题目内容
已知:如图,在正方形ABCD中,AD=1,P、Q分别为AD、BC上两点,且AP=CQ,连接AQ、BP交于点E,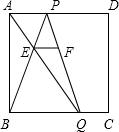 EF平行BC交PQ于F,AP、BQ分别为方程x2-mx+n=0的两根.
EF平行BC交PQ于F,AP、BQ分别为方程x2-mx+n=0的两根.(1)求m的值;
(2)试用AP、BQ表示EF;
(3)若S△PQE=
| 1 | 8 |
分析:(1)根据AP=QC,AP+BQ=QC+BQ=BC=1,AP、BQ分别为方程x2-mx+n=0的两根,可知AP+BQ=m,AP•BQ=n,所以AP+BQ=m=1;
(2)利用平行线等分线段定理,结合合比性质可求得
=
,
=
即
=
,所以EF=
;
(3)连接QD,则EP∥QD,得:S△AQD=
,三角形的面积公式,可知S△AEP=AP2•S△AQD=
AP2,所以求得S△PQE:S△AEP=EQ:AE,则可求得AP•BQ=
即n=
.
(2)利用平行线等分线段定理,结合合比性质可求得
| EQ |
| AE |
| BQ |
| AP |
| EQ |
| AE+EQ |
| BQ |
| AP+BQ |
| EQ |
| AQ |
| BQ |
| AP+BQ |
| AP•BQ |
| AP+BQ |
(3)连接QD,则EP∥QD,得:S△AQD=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
解答:解:(1)∵AP=QC,AP+BQ=QC+BQ=BC=1,
又∵AP、BQ分别为方程x2-mx+n=0的两根,
所以有AP+BQ=m,AP•BQ=n,
∴AP+BQ=m=1.
即m=1.
(2)∵EF∥AP,
∴
=
,
又∵AP∥BQ,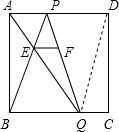
∴
=
,
∴
=
即
=
,
∴
=
,即:EF=
.
∵AP+BQ=1,
∴EF=AP•BQ.
(3)连接QD,则EP∥QD
得:S△AQD=
,
且S△AEP:S△AQD=AP2:AD2=AP2:1=AP2,
∴S△AEP=AP2•S△AQD=
AP2,
∴S△PQE:S△AEP=EQ:AE,
即
:
AP2=EQ:AE=BQ:AP,
∴AP•BQ=
,即:n=
.
又∵AP、BQ分别为方程x2-mx+n=0的两根,
所以有AP+BQ=m,AP•BQ=n,
∴AP+BQ=m=1.
即m=1.
(2)∵EF∥AP,
∴
| EF |
| AP |
| EQ |
| AQ |
又∵AP∥BQ,

∴
| EQ |
| AE |
| BQ |
| AP |
∴
| EQ |
| AE+EQ |
| BQ |
| AP+BQ |
| EQ |
| AQ |
| BQ |
| AP+BQ |
∴
| EF |
| AP |
| BQ |
| AP+BQ |
| AP•BQ |
| AP+BQ |
∵AP+BQ=1,
∴EF=AP•BQ.
(3)连接QD,则EP∥QD
得:S△AQD=
| 1 |
| 2 |
且S△AEP:S△AQD=AP2:AD2=AP2:1=AP2,
∴S△AEP=AP2•S△AQD=
| 1 |
| 2 |
∴S△PQE:S△AEP=EQ:AE,
即
| 1 |
| 8 |
| 1 |
| 2 |
∴AP•BQ=
| 1 |
| 4 |
| 1 |
| 4 |
点评:主要考查了正方形的性质和平行线等分线段定理和根与系数的关系.要会利用一元二次方程根与系数的关系得到对应的字母的值,灵活的运用正方形的性质和平行线等分线段定理中的比例线段求对应线段的值或比例关系.

练习册系列答案
 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
 已知:如图,在正方形ABCD中,E是CB延长线上一点,EB=
已知:如图,在正方形ABCD中,E是CB延长线上一点,EB= 已知:如图,在正方形ABCD外取一点E,连接AE、BE、DE.过点A作AE的垂线交DE于点P.若AE=AP=1,PB=
已知:如图,在正方形ABCD外取一点E,连接AE、BE、DE.过点A作AE的垂线交DE于点P.若AE=AP=1,PB= 已知:如图,在正方形ABCD中,P是BC上的点,且BP=3PC,Q是CD的中点.△ADQ与△QCP是否相似?
已知:如图,在正方形ABCD中,P是BC上的点,且BP=3PC,Q是CD的中点.△ADQ与△QCP是否相似? 、CE、CB于点F、H、G,交AB的延长线于点P.
、CE、CB于点F、H、G,交AB的延长线于点P. 已知:如图,在正方形ABCD中,E、F分别是AD、CD的中点.
已知:如图,在正方形ABCD中,E、F分别是AD、CD的中点.