题目内容

已知0＜a＜1，且[a+
1
30
]+[a+
2
30
]+…+[a+
29
30
]=18，求[10a]的值．
考点：取整计算
专题：计算题
分析：由于0＜a＜1，则a+
n
30
的值只能在0～1或1～2之间（n为1到29的整数），根据取整计算得到[a+
n
30
]的值只能为0或1，由于[a+
1
30
]+[a+
2
30
]+…+[a+
29
30
]=18，则前面11个数都为0，后面18个数都为1，于是得到0＜a+
11
30
＜1，1＜a+
12
30
＜2，解不等式组得到
18
30
＜a＜
19
30
，即6＜10a＜6.
•
3
，然后根据取整计算即可得到[10a]的值．
解答：解：∵0＜a＜1，
∴0＜a+
n
30
＜1或1＜a+
n
30
＜2（n为1到29的整数），
∴[a+
n
30
]=0或[a+
n
30
]=1，
∵[a+
1
30
]+[a+
2
30
]+…+[a+
29
30
]=18，
∴[a+
1
30
]=…=[a+
11
30
]=0，[a+
12
30
]=…=[a+
29
30
]=1，
∴0＜a+
11
30
＜1，1＜a+
12
30
＜2，
∴0＜a＜
19
30
，
18
30
＜a＜1，
∴
18
30
＜a＜
19
30
，
∴6＜10a＜6.
•
3
，
∴[10a]=6．
点评：本题考查了取整计算：[x]表示不大于x的最大整数．
练习册系列答案
相关题目
设an=500+n2，n为给定的自然数．对于任意非负整数n，记f（n）为an，an+1的最大公约数．试求f（n）的所有可能值．
已知△ABC中，AD与BE交于点F，且AE：EC=3：2，BD：BC=1：3，求S△ABF：S四边形DCEF．
解分式方程：5+
88
x2-16
=
2x-1
x+4
-
3x-1
4-x
．
已知S=
1
1
1949
+
1
1950
+
1
1951
+…+
1
2008
，求S的整数部分．
如图，在△ABC中，点E，F分别在边AB，AC上，EF∥BC，若△ABC的面积为1，S△AEF=2S△EBC，则S△CEF为
 
．
不等式组
3x-5
2
≤ x-2a
3(x-1)＜4(x+1)-3
有六个整数解，则a的取值范围为
 
．
如图在抛物线y=x（a-x）（a＞0）与x轴所围图形的内接矩形ABCD（边BC在x轴上）中，当矩形周长最大时，它的两边长AB=
 
，BC=
 
．
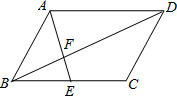?ABCD中，E是BC的中点，AE=9，BD=12，AD=10，则△ABD的面积为（　　）
A、24B、30C、36D、40

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网