题目内容
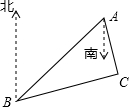如图，经测量，B处在A处的南偏西57°的方向，C处在A处的南偏东15°方向，C处在B处的北偏东82°方向，求∠C的度数．考点：方向角,三角形内角和定理
专题：
分析：根据平行线的性质，可得内错角相等，根据角的和差，可得∠ABC、∠BAC，根据三角形的内角和公式，可得答案．
解答：
解：因为BD∥AE，
所以∠DBA=∠BAE=57°．
所以∠ABC=∠DBC-∠DBA=82°-57°=25°．
在△ABC中，∠BAC=∠BAE+∠CAE=57°+15°=72°，
所以∠C=180°-∠ABC-∠BAC=180°-25°-72°=83°．
解：因为BD∥AE，所以∠DBA=∠BAE=57°．
所以∠ABC=∠DBC-∠DBA=82°-57°=25°．
在△ABC中，∠BAC=∠BAE+∠CAE=57°+15°=72°，
所以∠C=180°-∠ABC-∠BAC=180°-25°-72°=83°．
点评：本题考查了方向角，方向角是相互的，先求出∠ABC、∠BAC，再求出答案．
练习册系列答案
相关题目
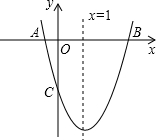如图，已知抛物线y=ax2+bx+c（a≠0）的对称轴为x=1，且抛物线经过A（-1，0）、C（0，-3）两点，与x轴交于另一点B．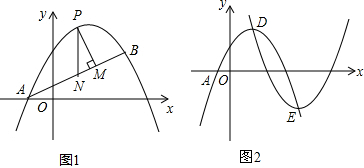
如图，已知：在△ABC中，AB=AC，BD是AC边上的中线，AB=13，BC=10，