题目内容
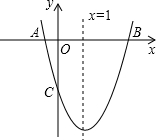 如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为x=1,且抛物线经过A(-1,0)、C(0,-3)两点,与x轴交于另一点B.
如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为x=1,且抛物线经过A(-1,0)、C(0,-3)两点,与x轴交于另一点B.(1)求这条抛物线所对应的函数关系式;
(2)在抛物线的对称轴直线x=1上找到一点M,使△ACM周长最小,请求出此时点M的坐标;
(3)在(2)的条件下,在x轴上找一点P,使得△APM是等腰三角形,请直接写出所有符合条件的点P的坐标.
考点:二次函数综合题
专题:
分析:(1)根据抛物线的对称轴可求出B点的坐标,进而可用待定系数法求出抛物线的解析式;
(2)由于A、B关于抛物线的对称轴直线对称,若连接BC,那么BC与直线x=1的交点即为所求的点M;可先求出直线BC的解析式,联立抛物线对称轴方程即可求得M点的坐标;
(3)根据△APM为等腰直角三角形,分别利用当AM=AP2时,当PM=AM时,当AP3=AM时,当AP1=MP1时求出即可.
(2)由于A、B关于抛物线的对称轴直线对称,若连接BC,那么BC与直线x=1的交点即为所求的点M;可先求出直线BC的解析式,联立抛物线对称轴方程即可求得M点的坐标;
(3)根据△APM为等腰直角三角形,分别利用当AM=AP2时,当PM=AM时,当AP3=AM时,当AP1=MP1时求出即可.
解答:解:(1)∵抛物线的对称轴为x=1,且A(-1,0),
∴B(3,0);
可设抛物线的解析式为y=a(x+1)(x-3),由于抛物线经过C(0,-3),
则有:a(0+1)(0-3)=-3,a=1;
∴y=(x+1)(x-3)=x2-2x-3;
(2)由于A、B关于抛物线的对称轴直线x=1对称,
那么M点为直线BC与x=1的交点;
由于直线BC经过C(0,-3),可设其解析式为y=kx-3,
则有:3k-3=0,k=1;
∴直线BC的解析式为y=x-3;
当x=1时,y=x-3=-2,
即M(1,-2);
(3)∵A(-1,0),M(1,-2),
∴AM=2
,
∴当AM=AP2=2
时,
则P2(2
-1,0),
当PM=AM时,P(3,0),
当AP3=AM时,则P3(-2
-1,0),
当AP1=MP1时,则P1(1,0),
综上所述:符合题意的P点坐标为:(2
-1,0),(3,0),(-2
-1,0),(1,0).
∴B(3,0);
可设抛物线的解析式为y=a(x+1)(x-3),由于抛物线经过C(0,-3),
则有:a(0+1)(0-3)=-3,a=1;
∴y=(x+1)(x-3)=x2-2x-3;
(2)由于A、B关于抛物线的对称轴直线x=1对称,
那么M点为直线BC与x=1的交点;
由于直线BC经过C(0,-3),可设其解析式为y=kx-3,
则有:3k-3=0,k=1;
∴直线BC的解析式为y=x-3;

当x=1时,y=x-3=-2,
即M(1,-2);
(3)∵A(-1,0),M(1,-2),
∴AM=2
| 2 |
∴当AM=AP2=2
| 2 |
则P2(2
| 2 |
当PM=AM时,P(3,0),
当AP3=AM时,则P3(-2
| 2 |
当AP1=MP1时,则P1(1,0),
综上所述:符合题意的P点坐标为:(2
| 2 |
| 2 |
点评:此题考查了二次函数解析式的确定、轴对称的性质以及等腰三角形的性质等知识,利用分类讨论得出是解题关键.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
 如图,已知直线y=-
如图,已知直线y=-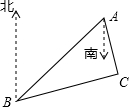 如图,经测量,B处在A处的南偏西57°的方向,C处在A处的南偏东15°方向,C处在B处的北偏东82°方向,求∠C的度数.
如图,经测量,B处在A处的南偏西57°的方向,C处在A处的南偏东15°方向,C处在B处的北偏东82°方向,求∠C的度数.