题目内容
已知:在△ABC中,∠ACB=90°,AC=BC,点D是AB的中点,点E是AB边上一点.
(1)直线BF垂直于CE于点F,交CD于点G(如图1).求证:AE=CG;
(2)直线AH垂直于CE,垂足为H,交CD的延长线于点M(如图2).那么图中是否存在与AM相等的线段?若存在,请写出来并证明;若不存在,请说明理由.
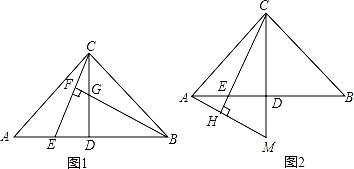
【考点】全等三角形的判定与性质.
【分析】(1)根据题意得到三角形ABC为等腰直角三角形,且CD为斜边上的中线,利用三线合一得到CD垂直于AB,且CD为角平分线,得到∠CAE=∠BCG=45°,再利用同角的余角相等得到一对角相等,AC=BC,利用ASA得到△AEC与△CGB全等,利用全等三角形的对应边相等即可得证.
(2)图中存在与AM相等的线段,AM=CE.先证出∠CEB=∠CMA,再由AAS证明△BCE≌△ACM,即可解答.
【解答】解:(1)∵点D是AB的中点,AC=BC,∠ACB=90°,
∴CD⊥AB,∠ACD=∠BCD=45°,∠CAD=∠CBD=45°.
∴∠CAE=∠BCG.
∵BF⊥CE,
∴∠CBG+∠BCF=90°.
∵∠ACE+∠BCF=90°,
∴∠ACE=∠CBG.
在△AEC和△CGB中,
 ,
,
∴△AEC≌△CGB(ASA).
∴AE=CG.
(2)图中存在与AM相等的线段,AM=CE.
证明:∵CH⊥HM,CD⊥ED,
∴∠CMA+∠MCH=90°,∠BEC+∠MCH=90°.
∴∠CMA=∠BEC.
∵AC=BC,∠ACM=∠CBE=45°,
在△CAM和△BCE中,
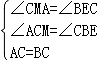 ,
,
∴△CAM≌△BCE(AAS).
∴AM=CE.
【点评】本题考查了全等三角形的判定与性质;熟练掌握全等三角形的判定方法是解决问题的关键.

每年9月举行“全国中学生数学联赛”,成绩优异的选手可参加“全国中学生数学冬令营”,冬令营再选拔出50名优秀选手进入“国家集训队”.第31界冬令营已于2015年12月在江西省鹰谭一中成功举行.现将脱颖而出的50名选手分成两组进行竞赛,每组25人,成绩整理并绘制成如下的统计图: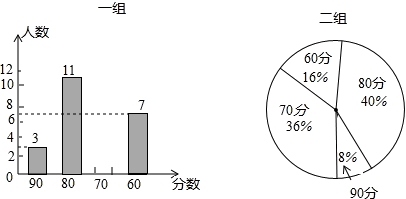
请你根据以上提供的信息解答下列问题:
(1)请你将表格补充完整:
| 平均数 | 中位数 | 众数 | 方差 | |
| 一组 | 74 | __________ | __________ | 104 |
| 二组 | __________ | __________ | __________ | 72 |
(2)从本次统计数据来看,__________组比较稳定.

 的图象经过(﹣2,5),则该反比例函数的图象在( )
的图象经过(﹣2,5),则该反比例函数的图象在( ) ,然后在0,1,2,3中选择一个你喜欢的a值,代入求值.
,然后在0,1,2,3中选择一个你喜欢的a值,代入求值.


 B.
B.
 C.
C.
 D.
D.


 +
+
 )÷
)÷