题目内容
13.已知关于x的方程x2+2mx+m-1=0(1)若该方程的一个根为-2,求m的值及该方程的另一根;
(2)求证:不论m取何实数,该方程都有两个不相等的实数根.
分析 (1)直接把x=-2代入方程x2+2mx+m-1=0求出m的值,故可得出方程,求出方程的解即可;
(2)求出△的值,再比较出其大小即可.
解答 (1)解:将x=-2代入方程x2+2mx+m-1=0得,
4-4m+m-1=0,解得m=1;
方程为x2+2x=0,解得x=0或-2,
即另一根为0;
(2)证明:∵△=4m2-4(m-1)=(2m-1)2+3≥3>0,
∴不论m取何实数,该方程都有两个不相等的实数根.
点评 本题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2-4ac:当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.同时考查了一元二次方程的解的定义以及一元二次方程的解法.

练习册系列答案
相关题目
2.用配方法解方程a2-4a-1=0,下列配方正确的是( )
| A. | (a-2)2-4=0 | B. | (a+2)2-5=0 | C. | (a+2)2-3=0 | D. | (a-2)2-5=0 |
3.某公司全体员工年薪的具体情况如表:
则所有员工的年薪平均数比中位数多2万元.
| 年薪/万元 | 30 | 14 | 9 | 6 | 4 | 3.5 |
| 员工数/人 | 1 | 1 | 1 | 2 | 7 | 6 |
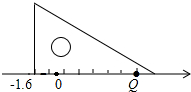 慧慧自己做了一个三角形的纸片,并在其中的一边画了七个长度相等的小格,每小格的长度为1个单位长度,然后把此边放在如图所示的数轴上,则点Q所表示的数是5.4.
慧慧自己做了一个三角形的纸片,并在其中的一边画了七个长度相等的小格,每小格的长度为1个单位长度,然后把此边放在如图所示的数轴上,则点Q所表示的数是5.4.