题目内容
已知|x|=
,|y|=
,且xy>0,则x-y= .
| 3 |
| 2 |
| 1 |
| 2 |
考点:代数式求值,绝对值
专题:
分析:先根据绝对值的性质求出x、y的值,再根据xy>0确定x、y是同号,分类求出x-y的值.
解答:解:∵|x|=
,|y|=
,
∴x=±
,y=±
,
∵xy>0,∴x、y同号,
∴当x=
,y=
时,x-y=
-
=1;
当x=-
,y=-
时,x-y=-
-(-
)=-1;
故答案为:±1.
| 3 |
| 2 |
| 1 |
| 2 |
∴x=±
| 3 |
| 2 |
| 1 |
| 2 |
∵xy>0,∴x、y同号,
∴当x=
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
当x=-
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
故答案为:±1.
点评:本题考查了绝对值的性质;根据题意确定x、y啥同号是解题的关键;注意分类讨论.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下列说法中,正确的是( )
| A、两条射线组成的图形叫做角 |
| B、两点确定一条直线 |
| C、两点之间直线最短 |
| D、若AB=BC,则点B是AC的中点 |
下列式子中的y不是x的函数的是( )
| A、y=-2x-3 | ||
B、y=-
| ||
C、y=±
| ||
| D、y=x+1 |
如果(x-4)(x+3)=x2+mx-n,那么m、n的值分别是( )
| A、1、12 |
| B、-1、-12 |
| C、1、-12 |
| D、-1、12 |
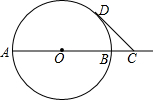 如图,已知AB是⊙O的直径,AB=4,点C在线段AB的延长线上,点D在⊙O上,连接CD,且CD=OA,OC=2
如图,已知AB是⊙O的直径,AB=4,点C在线段AB的延长线上,点D在⊙O上,连接CD,且CD=OA,OC=2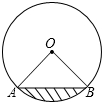 如图,水平放置的圆柱形排水管道的横截面半径是2
如图,水平放置的圆柱形排水管道的横截面半径是2