题目内容
不透明的口袋里装有红、黄、蓝三种颜色的小球若干个(除颜色外其余都相同),其中红球2个(分别标有1号、2号),蓝球1个.若从中任意摸出一个球,它是蓝球的概率为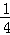 .
.
(1)求袋中黄球的个数;
(2)第一次任意摸出一个球(不放回),第二次再摸出一个球,请用画树状图或列表格的方法,求两次摸到不同颜色球的概率.
【考点】列表法与树状图法;概率公式.
【分析】(1)利用概率的求解方法,借助于方程求解即可;
(2)此题需要两步完成,所以采用树状图法或者采用列表法都比较简单;解题时要注意是放回实验还是不放回实验,此题属于不放回实验.
【解答】解:(1)设袋中黄球的个数为x个,
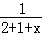 =
=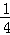
∴x=1
∴袋中黄球的个数为 1个;(
1个;( 2分)
2分)
(2)方法一、列表如下:(6分)
| * | 红1 | 红2 | 黄 | 蓝 |
| 红1 | * | (红1,红2) | (红1,黄) | (红1,蓝) |
| 红2 | (红2,红1) | * | (红2,黄) | (红2,蓝) |
| 黄 | (黄,红1) | (黄,红2) | * | (黄,蓝) |
| 蓝 | (蓝,红1) | (蓝,红2) | (蓝,黄) | * |
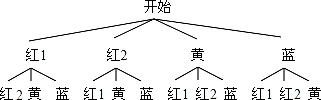
∴一共有12种情况,两次摸到不同颜色球的有10种情况,
∴两次摸到不同颜色球的概率为: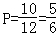 .(8分)
.(8分)
方法二,画树状图如下:
【点评】(1)注意利用方程思想,掌握概率公式的求法;
(2)此题考查的是用列表法或树状图法求概率.列表法可以不重复不遗漏的列出所有可能的结果,适合于两步完成的事件;树状图法适合两步或两步以上完成的事件;解题时要注意此题是放回实验还是不放回实验.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
相关题目

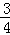 x2+mx+n经过点A和点C.且与x轴交于点B,动点P在x轴上以每秒1个单位长度的速度由点B向点A运动.点Q由点C沿线段CA向点A运动.且速度是点P运动速度的2倍.
x2+mx+n经过点A和点C.且与x轴交于点B,动点P在x轴上以每秒1个单位长度的速度由点B向点A运动.点Q由点C沿线段CA向点A运动.且速度是点P运动速度的2倍.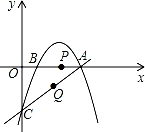


 在第一象限的图象与BC相交于点M,交AB于N,若已知S△MBN=9,则k的值为 .
在第一象限的图象与BC相交于点M,交AB于N,若已知S△MBN=9,则k的值为 .