题目内容
 如图所示,在高为150m的山顶D上测得某塔的塔顶A与塔基B的俯角分别为30°和45°,求塔高AB.(精确到0.1m,参考数据:
如图所示,在高为150m的山顶D上测得某塔的塔顶A与塔基B的俯角分别为30°和45°,求塔高AB.(精确到0.1m,参考数据: ≈1.414,
≈1.414, ≈1.732)
≈1.732)
 解:过点A作AE⊥CD于点E,
解:过点A作AE⊥CD于点E,在Rt△CBD中,∠CBD=45°,
∴CD=CB=150m,
在Rt△DEA中,∠DAE=30°,
∴DE=AE•tan30°=150×
 =50
=50 ≈86.60(m).
≈86.60(m).∴AB=CE=CD-DE=150-86.60=63.4(m).
答:塔高AB约为63.4m.
分析:首先过点A作AE⊥CD于点E,在Rt△CBD中,由∠CBD=45°,可得CD=CB=150m,然后在Rt△DEA中,由∠DAE=30°,求得DE的长,继而求得答案.
点评:此题考查了俯角的定义.注意能借助俯角构造直角三角形并解直角三角形是解此题的关键.

练习册系列答案
相关题目
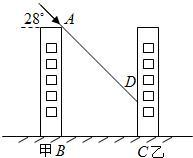 小,最小夹角约为28度.现有两幢居民住宅楼高为15米,两楼相距20米,如图所示.
小,最小夹角约为28度.现有两幢居民住宅楼高为15米,两楼相距20米,如图所示.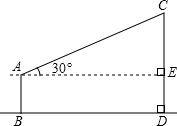 (2013•石峰区模拟)如图所示,小明测量学校旗杆的高度,他在离电线杆CD距离为15米的地方放置一个高1.5米的测角仪(AB),此时,经A处测得旗杆上顶端C处的仰角为30°.请问:这样就能够测出旗杆CD的高度吗?如果能,CD的高是多少米?(结果精确到0.1)
(2013•石峰区模拟)如图所示,小明测量学校旗杆的高度,他在离电线杆CD距离为15米的地方放置一个高1.5米的测角仪(AB),此时,经A处测得旗杆上顶端C处的仰角为30°.请问:这样就能够测出旗杆CD的高度吗?如果能,CD的高是多少米?(结果精确到0.1) (2012•孝感模拟)在数学课外小组活动中,小红同学用纸板制作了一个圆锥形漏斗模型.如图所示,它的底面直径为6,高为4.则这个圆锥漏斗的侧面积是( )
(2012•孝感模拟)在数学课外小组活动中,小红同学用纸板制作了一个圆锥形漏斗模型.如图所示,它的底面直径为6,高为4.则这个圆锥漏斗的侧面积是( ) (2013•太原二模)某一时刻,一建筑物的影子恰好落在水平地面和一斜坡上,如图所示,此时测得地面上的影长AC为15米,坡面上的影长CD为10米.已知斜坡的坡角(即∠DCF)为45°,在点D处观测该建筑物顶部点B的仰角(即∠BDE)也恰好为45°,点A,B,C,D在同一平面内,此建筑物的高AB为( )
(2013•太原二模)某一时刻,一建筑物的影子恰好落在水平地面和一斜坡上,如图所示,此时测得地面上的影长AC为15米,坡面上的影长CD为10米.已知斜坡的坡角(即∠DCF)为45°,在点D处观测该建筑物顶部点B的仰角(即∠BDE)也恰好为45°,点A,B,C,D在同一平面内,此建筑物的高AB为( ) 如图所示,课外活动中,小明在离旗杆AB的10米C处,用测角仪测得旗杆顶部A的仰角为40°,已知测角仪器的高CD=15米,求旗杆AB的高.(精确到0.1米)
如图所示,课外活动中,小明在离旗杆AB的10米C处,用测角仪测得旗杆顶部A的仰角为40°,已知测角仪器的高CD=15米,求旗杆AB的高.(精确到0.1米)