题目内容
6.已知正方形ABCD的边长是4,对角线交于点O,F为BC上一点,连接OF、AF,若OF=$\sqrt{5}$,则线段AF的长度的是$\sqrt{17}$或5.分析 过点O作BC的垂线,垂足为E.根据正方形的性质得出OA=OC,∠ABC=90°,又OE∥AB,得出BE=EC=$\frac{1}{2}$BC=2,OE=$\frac{1}{2}$AB=2.在Rt△OEF中利用勾股定理求出EF=1.再分两种情况讨论:①F在线段BE上;②F在线段CE上,分别求出BF的长,由勾股定理求出AF的长.
解答 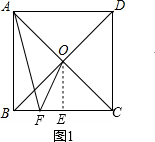 解:过点O作BC的垂线,垂足为E.
解:过点O作BC的垂线,垂足为E.
∵四边形ABCD是正方形,
∴OA=OC,∠ABC=90°,
∵OE⊥BC,
∴OE∥AB,
∴BE=EC=$\frac{1}{2}$BC=2,OE=$\frac{1}{2}$AB=2.
∵在Rt△OEF中,∠OEB=90°,OF=$\sqrt{5}$,OE=2,
∴EF=$\sqrt{O{F}^{2}-O{E}^{2}}$=1.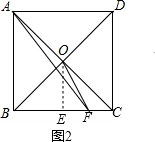 分两种情况讨论:
分两种情况讨论:
①F在线段BE上时,如图1,
此时BF=BE-EF=2-1=1,
在Rt△ABF中,∵AB=4,BF=1,
∴AF=$\sqrt{{AB}^{2}+B{F}^{2}}$=$\sqrt{17}$;
②F在线段CE上时,如图2,
此时BF=BE+EF=2+1=3,
在Rt△ABF中,∵AB=4,BF=3,
∴AF=$\sqrt{{AB}^{2}+B{F}^{2}}$=5;
故答案为:$\sqrt{17}$或5.
点评 本题考查了正方形的性质,勾股定理,熟练掌握正方形的性质和勾股定理,利用数形结合与分类讨论是解题的关键.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
12.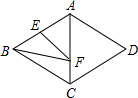 如图,菱形ABCD的边长为4,∠BAD=120°,点E是AB的中点,点F是AC上的一动点,则EF+BF的最小值是( )
如图,菱形ABCD的边长为4,∠BAD=120°,点E是AB的中点,点F是AC上的一动点,则EF+BF的最小值是( )
 如图,菱形ABCD的边长为4,∠BAD=120°,点E是AB的中点,点F是AC上的一动点,则EF+BF的最小值是( )
如图,菱形ABCD的边长为4,∠BAD=120°,点E是AB的中点,点F是AC上的一动点,则EF+BF的最小值是( )| A. | 4 | B. | 2$\sqrt{3}$ | C. | 4$\sqrt{3}$ | D. | 2$\sqrt{7}$ |
 如图,已知菱形ABCD的周长为16,∠B=120°,求这个菱形的面积.
如图,已知菱形ABCD的周长为16,∠B=120°,求这个菱形的面积.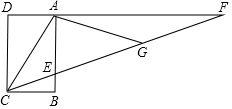 “三等分一个任意角”是数学史上一个著名问题,今天人们已经知道,仅用圆规直尺是不可能做出的.在探索中,有人曾利用过如图所示的图形,其中,ABCD是长方形(AD∥CB),F是DA延长线上一点,G 是CF上一点,并且∠ACG=∠AGC,∠GAF=∠F,你能证明∠ECB=$\frac{1}{3}$∠ACB吗?
“三等分一个任意角”是数学史上一个著名问题,今天人们已经知道,仅用圆规直尺是不可能做出的.在探索中,有人曾利用过如图所示的图形,其中,ABCD是长方形(AD∥CB),F是DA延长线上一点,G 是CF上一点,并且∠ACG=∠AGC,∠GAF=∠F,你能证明∠ECB=$\frac{1}{3}$∠ACB吗?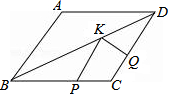 如图,菱形ABCD中,AB=3,∠A=120°,点P,Q,K分别为线段BC,CD,BD上的任意一点,则PK+QK的最小值为$\frac{3\sqrt{3}}{2}$.
如图,菱形ABCD中,AB=3,∠A=120°,点P,Q,K分别为线段BC,CD,BD上的任意一点,则PK+QK的最小值为$\frac{3\sqrt{3}}{2}$.