题目内容
将正方形ABCD(如下图1)作如下划分：
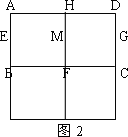
第1次划分：分别联结正方形ABCD对边的中点(如图2)，得线段HF和EG，它们交于点M，此时图2中共有5个正方形；
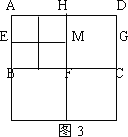
第2次划分：将图2左上角正方形AEMH按上述方法再作划分，得图3，则图3中共有________个正方形；
若每次都把左上角的正方形依次划分下去，则第100次划分后，图中共有________个正方形；
继续划分下去，能否将正方形ABCD划分成有2011个正方形的图形？需说明理由．
答案：
解析：
解析：
|
第2次划分，共有9个正方形； 1分 第100次划分后，共有401个正方形； 2分 依题意，第n次划分后，图中共有4n＋1个正方形， 3分 而方程4n＋1＝2011没有整数解， 所以，不能得到2011个正方形． 4分 |
练习册系列答案
相关题目
如图，等腰梯形MNPQ的上底长为2，腰长为3，一个底角为60°．正方形ABCD的边长为1，它的一边AD在MN上，且顶点A与M重合．现将正方形ABCD在梯形的外面沿边MN、NP、PQ进行翻滚，翻滚到有一个顶点与Q重合即停止滚动．正方形在整个翻滚过程中点A所经过的路线与梯形MNPQ的三边MN、NP、PQ所围成图形的面积S是