题目内容
给出下列几组数:①4,5,6;②8,15,16;③n2-1,2n,n2+1;④m2-n2,2mn,m2+n2(m>n>0).其中一定能组成直角三角形三边长的是( )
| A、①② | B、③④ | C、①③④ | D、④ |
考点:勾股定理的逆定理
专题:
分析:根据勾股定理的逆定理逐个判断即可.
解答:解:∵42+52≠62,即三角形不是直角三角形,∴①错误;
∵82+152≠162,即三角形不是直角三角形,∴②错误;
∵(n2-1)2+(2n)2=(n2+1)2,即三角形是直角三角形,∴③正确;
∵(m2-n2)2+(2mn)2=(m2+n2)2,即三角形是直角三角形,∴④正确;
故选B.
∵82+152≠162,即三角形不是直角三角形,∴②错误;
∵(n2-1)2+(2n)2=(n2+1)2,即三角形是直角三角形,∴③正确;
∵(m2-n2)2+(2mn)2=(m2+n2)2,即三角形是直角三角形,∴④正确;
故选B.
点评:本题考查了对勾股定理的逆定理的应用,注意:如果一个三角形的两边a、b的平方和等于第三边c的平方,那么这个三角形是直角三角形.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
 平行四边形一边长为10,那么它的对角线长度和可以为( )
平行四边形一边长为10,那么它的对角线长度和可以为( )| A、8和12 | B、20和30 |
| C、6和8 | D、4和6 |
下列式子正确的是( )
| A、2>0>-4>-1 |
| B、-4>-1>2>0 |
| C、-4<-1<0<2 |
| D、0<2>-1<-4 |
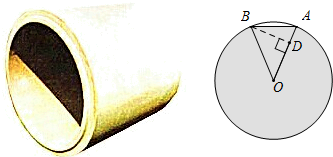
 如图,已知AB是半圆O的直径,∠BAC=32°,D是弧AC的中点,求∠DAC的度数.
如图,已知AB是半圆O的直径,∠BAC=32°,D是弧AC的中点,求∠DAC的度数.