题目内容
11. 打高尔夫球时,球的飞行路线可以看成是一条抛物线,如果不考虑空气的阻力,某次球的飞行高度y(单位:米)与飞行距离x(单位:百米)满足二次函数:y=-5x2+20x,这个球飞行的水平距离最远是多少米?球的飞行高度能否达到40m?
打高尔夫球时,球的飞行路线可以看成是一条抛物线,如果不考虑空气的阻力,某次球的飞行高度y(单位:米)与飞行距离x(单位:百米)满足二次函数:y=-5x2+20x,这个球飞行的水平距离最远是多少米?球的飞行高度能否达到40m?
分析 当高度y=0时,球飞行的水平距离最大.对于y=-5x2+20x,令y=0,得到关于x的方程,解方程即可,把y=-5x2+20x配成抛物线的顶点式,然后根据二次函数的最值问题进行回答即可.
解答 解:令y=0,
即:-5x2+20x=0,解得x1=0,x2=4,
所以这次击球,球飞行的最大水平距离是4米;
∵y=-5x2+20x=-5(x-2)2+20,
∴球的飞行高度最大是20米,
∴球的飞行高度不能达到40m.
点评 本题考查了二次函数的应用:先把二次函数关系式变形成顶点式:y=a(x-k)2+h,当a<0,x=k时,y有最大值h;当a>0,x=k时,y有最小值h.

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案
相关题目
1. 如图,AD∥BE∥CF,直线l1、l2与这三条平行线分别交于点A、B、C和点D、E、F.若AB=4.5,BC=3,EF=2,则DE的长度是( )
如图,AD∥BE∥CF,直线l1、l2与这三条平行线分别交于点A、B、C和点D、E、F.若AB=4.5,BC=3,EF=2,则DE的长度是( )
 如图,AD∥BE∥CF,直线l1、l2与这三条平行线分别交于点A、B、C和点D、E、F.若AB=4.5,BC=3,EF=2,则DE的长度是( )
如图,AD∥BE∥CF,直线l1、l2与这三条平行线分别交于点A、B、C和点D、E、F.若AB=4.5,BC=3,EF=2,则DE的长度是( )| A. | $\frac{4}{3}$ | B. | 3 | C. | 5 | D. | $\frac{27}{4}$ |
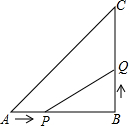 如图,在△ABC中,∠B=90°,AB=6cm,BC=6cm,点P从点A出发沿AB边向点B以1cm/秒的速度移动,点Q从点B出发沿BC边向点C以2cm/秒的速度移动.
如图,在△ABC中,∠B=90°,AB=6cm,BC=6cm,点P从点A出发沿AB边向点B以1cm/秒的速度移动,点Q从点B出发沿BC边向点C以2cm/秒的速度移动.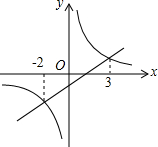 如图,一次函数y1=kx+b图象与反比例函数y2=$\frac{m}{x}$图象的两交点横坐标分别为-2、3,观察图象,写出y1>y2时,x的取值范围是-2<x<0,或x>3.
如图,一次函数y1=kx+b图象与反比例函数y2=$\frac{m}{x}$图象的两交点横坐标分别为-2、3,观察图象,写出y1>y2时,x的取值范围是-2<x<0,或x>3.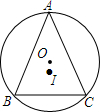 如图,△ABC中,AB=AC=13,BC=10,⊙O为△ABC外接圆,I为△ABC的内心.
如图,△ABC中,AB=AC=13,BC=10,⊙O为△ABC外接圆,I为△ABC的内心.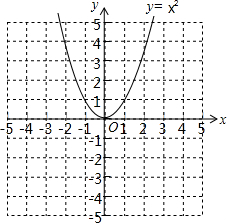 二次函数y=x2的图象如图,请将此图象向右平移1个单位,再向下平移4个单位.
二次函数y=x2的图象如图,请将此图象向右平移1个单位,再向下平移4个单位.