题目内容
2.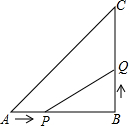 如图,在△ABC中,∠B=90°,AB=6cm,BC=6cm,点P从点A出发沿AB边向点B以1cm/秒的速度移动,点Q从点B出发沿BC边向点C以2cm/秒的速度移动.
如图,在△ABC中,∠B=90°,AB=6cm,BC=6cm,点P从点A出发沿AB边向点B以1cm/秒的速度移动,点Q从点B出发沿BC边向点C以2cm/秒的速度移动.(1)如果P、Q分别从A、B同时出发,那么△PBQ的面积S随出发时间t如何变化?请写出S关于t的函数解析式及t的取值范围.
(2)如果P、Q分别从A、B同时出发,经过多长时间,△PBQ的面积为8cm2?
(3)如果P、Q分别从A、B同时出发,当P、Q两点运动几秒时,PQ有最小值,并求这个最小值.
分析 (1)由题意,可设P、Q经过t秒,使△PBQ的面积为8cm2,则PB=6-t,BQ=2t,根据三角形面积的计算公式,S△PBQ=$\frac{1}{2}$BP×BQ,列出表达式,解答出即可;
(2)把S△PBQ=8代入求得相应的t的值即可;
(3)可设P、Q两点运动t秒时,PQ有最小值,则PB=6-t,BQ=2t,根据勾股定理,可得PQ2=BP2+BQ2,代入整理即可求出其最小值;
解答 解:(1)设P、Q经过t秒时,△PBQ的面积为8cm2,
则PB=6-t,BQ=2t,
∵∠B=90°,
∴S△PBQ=$\frac{1}{2}$BP×BQ=$\frac{1}{2}$(6-t)×2t=-t2+6t,即S=-t2+6t(0≤t≤6);
(2)由(1)得到S=-t2+6t.
当S=8时,-t2+6t=8,
解得,t1=2,t2=4,
∴当P、Q经过2或4秒时,△PBQ的面积为8cm2;
(2)设P、Q两点运动t秒时,PQ有最小值,
∴PQ2=(6-t)2+(2t)2,
整理得,PQ2=5(t-$\frac{6}{5}$)2+$\frac{144}{5}$,
∴当t=$\frac{6}{5}$时,PQ有最小值为:$\frac{12\sqrt{5}}{5}$.
点评 本题主要考查了一元二次方程的应用和二次函数及其最值,根据题意,正确表示出边长及配方法求出最值,是解答本题的关键.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
10.某商品连续两次降价,每次都降20%后的价格为36元,则原价是( )
| A. | 56.25元 | B. | 51.84元 | C. | 25元 | D. | 23.04元 |
17.若方程x2+ax+b=0中有一个根为0,另一个根非0,则a、b的值是( )
| A. | a=0,b=0 | B. | a≠0,b=0 | C. | a=0,b≠0 |
14.有一个数值转换器,原理如下:

当输入的x=9时,输出的y等于( )

当输入的x=9时,输出的y等于( )
| A. | 2 | B. | 8 | C. | $\sqrt{3}$ | D. | $±\sqrt{3}$ |
12. 如图,AB∥CD,∠D=∠E,若∠B=70°,则∠D的大小为( )
如图,AB∥CD,∠D=∠E,若∠B=70°,则∠D的大小为( )
 如图,AB∥CD,∠D=∠E,若∠B=70°,则∠D的大小为( )
如图,AB∥CD,∠D=∠E,若∠B=70°,则∠D的大小为( )| A. | 20° | B. | 25° | C. | 30° | D. | 35° |

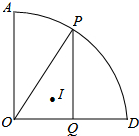 如图,扇形AOD中,∠AOD=90°,OA=8,点P为弧AD上一动点,PQ⊥OD于点Q,点I为△OPQ的内心,当点P从点A沿弧AD运动到点D时,点I运动的路径长为2$\sqrt{2}π$.
如图,扇形AOD中,∠AOD=90°,OA=8,点P为弧AD上一动点,PQ⊥OD于点Q,点I为△OPQ的内心,当点P从点A沿弧AD运动到点D时,点I运动的路径长为2$\sqrt{2}π$. 打高尔夫球时,球的飞行路线可以看成是一条抛物线,如果不考虑空气的阻力,某次球的飞行高度y(单位:米)与飞行距离x(单位:百米)满足二次函数:y=-5x2+20x,这个球飞行的水平距离最远是多少米?球的飞行高度能否达到40m?
打高尔夫球时,球的飞行路线可以看成是一条抛物线,如果不考虑空气的阻力,某次球的飞行高度y(单位:米)与飞行距离x(单位:百米)满足二次函数:y=-5x2+20x,这个球飞行的水平距离最远是多少米?球的飞行高度能否达到40m?