题目内容
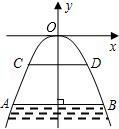
有一座抛物线形拱桥，在正常水位AB时，水面AB宽24 m，拱顶距离水面4 m。以抛物线的顶点为原点，以抛物线的对称轴为y轴，建立如图所示的平面直角坐标系。
（1）求抛物线的解析式；
（2）若水位上升3 m就达到警戒线CD的位置，求这时水面CD的宽度。
（1）求抛物线的解析式；
（2）若水位上升3 m就达到警戒线CD的位置，求这时水面CD的宽度。
解：（1） 设这条抛物线的解析式为y=ax2，
由已知抛物线经过点B (12，-4)
可得 -4=a
122，
有 a=
，
∴抛物线的解析式为 y=
x2
（2）由题意知，点D的纵坐标为-1，设点D的坐标为（x，-1）（x>0），
可得 -1=
x2，
解得 x=6
∴CD=2x=12（m）
答：这时水面宽度为12 m。
由已知抛物线经过点B (12，-4)
可得 -4=a
122，有 a=
，∴抛物线的解析式为 y=
x2 （2）由题意知，点D的纵坐标为-1，设点D的坐标为（x，-1）（x>0），
可得 -1=
x2，解得 x=6
∴CD=2x=12（m）
答：这时水面宽度为12 m。
练习册系列答案
相关题目
如图所示，有一座抛物线形拱桥，桥下面在正常水位AB时，宽20m，水位上升3m就达到警戒线CD，这时水面宽度为10m．
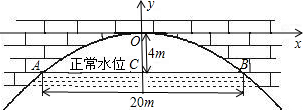
有一座抛物线形拱桥，桥下面在正常水位时AB宽20米，水位上升3米就达到警戒线CD，这时水面宽度为10米；