题目内容
有一座抛物线形拱桥,正常水位时桥下水面宽度为20米,拱顶距离水面4米.设正常水位时桥下的水深为2米,为保证过往船只顺利航行,桥下水面的宽度不得小于18米,则水深超过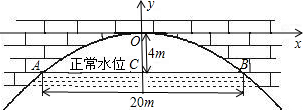
分析:以拱顶为坐标原点,水平向右为x轴正方向,建立平面直角坐标系.根据题中数据求出抛物线解析式.桥下水面的宽度不得小于18米,即求当x=9时y的值,然后根据正常水位进行解答.
解答:解:设抛物线解析式为y=ax2,
把点B(10,-4)代入解析式得:-4=a×102,
解得:a=-
,
∴y=-
x2,把x=9代入,得:
y=-
=-3.24,
此时水深=4+2-3.24=2.76米.
把点B(10,-4)代入解析式得:-4=a×102,
解得:a=-
| 1 |
| 25 |
∴y=-
| 1 |
| 25 |
y=-
| 81 |
| 25 |
此时水深=4+2-3.24=2.76米.
点评:本题考查点的坐标的求法及二次函数的实际应用.此题为数学建模题,借助二次函数解决实际问题.

练习册系列答案
 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目

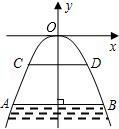 如图所示,有一座抛物线形拱桥,桥下面在正常水位AB时,宽20m,水位上升3m就达到警戒线CD,这时水面宽度为10m.
如图所示,有一座抛物线形拱桥,桥下面在正常水位AB时,宽20m,水位上升3m就达到警戒线CD,这时水面宽度为10m. 有一座抛物线形拱桥,桥下面在正常水位时AB宽20米,水位上升3米就达到警戒线CD,这时水面宽度为10米;
有一座抛物线形拱桥,桥下面在正常水位时AB宽20米,水位上升3米就达到警戒线CD,这时水面宽度为10米;