题目内容
14.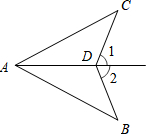 如图,∠1=∠2,那么添加一个条件后,仍无法判定△ABD≌△ACD的是( )
如图,∠1=∠2,那么添加一个条件后,仍无法判定△ABD≌△ACD的是( )| A. | AB=AC | B. | ∠B=∠C | C. | ADAD平分∠CAB | D. | CDCD=BD |
分析 根据全等三角形的判定方法进行分析即可.
解答 解:∵∠1=∠2,∴∠ADC=∠ADB,
A、AB=AC,AD=AD,∠ADC=∠ADB,仍无法判定△ABD≌△ACD,符合题意;
B、∠ADC=∠ADB,∠B=∠C,AD=AD,由AAS可以判定△ABD≌△ACD,不符合题意;
C、∵AD平分∠CAB,∴∠CAD=∠BAD,∵∠ADC=∠ADB,AD=AD,由ASA可以判定△ABD≌△ACD,不符合题意;
D、CD=BD,∠ADC=∠ADB,AD=AD,由SAS可以判定△ABD≌△ACD,不符合题意;
故选:A.
点评 本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.

练习册系列答案
相关题目
4.用配方法解方程x2-8x+15=0时,下列变形中,正确的是( )
| A. | (x-4)2=31 | B. | (x-4)2=1 | C. | (x-8)2=1 | D. | (x-8)2=31 |
2.“勤劳”是中华民族的传统美德,我校要求同学们在家里帮助父母做些力所能及的家务.王刚同学在本学期开学初对部分同学寒假在家做家务的时间进行了抽样调查(时间取整数小时),所得数据统计如表:
(1)抽取样本的容量是100.
(2)根据表中数据补全图中的频数分布直方图.
(3)样本的中位数所在时间段的范围是40.5~60.5.
(4)若我学校共有学生1600人,那么大约有多少学生在寒假做家务的时间在40.5~100.5小时之间?
| 时间分组 | 0.5~20.5 | 20.5~40.5 | 40.5~60.5 | 60.5~80.5 | 80.5~100.5 |
| 频 数 | 20 | 25 | 30 | 15 | 10 |
(2)根据表中数据补全图中的频数分布直方图.
(3)样本的中位数所在时间段的范围是40.5~60.5.
(4)若我学校共有学生1600人,那么大约有多少学生在寒假做家务的时间在40.5~100.5小时之间?

3.如图所示的各组图形中,表示平移关系的是( )
| A. |  | B. |  | C. |  | D. |  |
5.已知,二次函数y=ax2+bx+c与x轴的交点为(x1,0),(x2,0),且x1<x2,若方程ax2+bx+c-a=0的两根为m,n(m<n),则下列说法正确的是( )
| A. | x1+x2>m+n | B. | m<n<x1<x2 | C. | x1<m<n<x2 | D. | m<x1<x2<n |