Question

2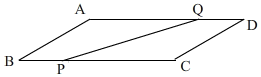．如图，在平行四边形ABCD中，AB=6cm，BC=12cm，∠B=30°，点P在BC上由点B向点C出发，速度为每秒2cm；点Q在边AD上，同时由点D向点A运动，速度为每秒1cm，当点P运动到点C时，P、Q同时停止运动，连接PQ，设运动时间为t秒．
（1）设四边形ABPQ的面积为y，求y与t之间的函数关系式；
（2）t为何值时四边形ABPQ为平行四边形？
（3）连结AP，是否存在某一时刻t，使△ABP为等腰三角形？并求出此刻t的值．

Answer 1

分析 （1）先构造直角三角形，求出AE，再用梯形的面积公式即可得出结论；
（2）利用平行四边形的对边相等AQ=BP建立方程求解即可；
（3）分三种情况，利用等腰三角形的性质，两腰相等建立方程求解即可得出结论．

解答 解：（1）如图1，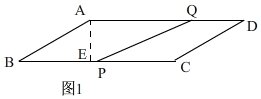
过点A作AE⊥BC于E，
在Rt△ABE中，∠B=30°，AB=6，
∴AE=3，
由运动知，BP=2t，DQ=t，
∵四边形ABCD是平行四边形，
∴AD=BC=12，
∴AQ=12-t，
∴y=S_{四边形ABPQ}=$\frac{1}{2}$（BP+AQ）•AE=$\frac{1}{2}$（2t+12-t）×3=$\frac{3}{2}$t+18（0＜t≤6）

（2）由（1）知，AQ=12-t，BP=2t，
∵四边形ABPQ为平行四边形，
∴AQ=BP，
∴12-t=2t   
∴t=4，
即：t=4s时，四边形ABPQ是平行四边形；

（3）①当AB=BP时，BP=6，
即2t=6，t=3；       
②当AP=BP时，如图2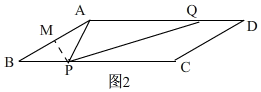，∠B=30°，
过P作PM垂直于AB，垂足为点M，
∴BM=3，BP=2$\sqrt{3}$，
∴2t=2$\sqrt{3}$，
∴t=$\sqrt{3}$
③当AB=AP时，同（2）的方法得，BP=6$\sqrt{3}$，
∴2t=6$\sqrt{3}$，
∴t=3$\sqrt{3}$
所以，当t=3或$\sqrt{3}$ 或3$\sqrt{3}$时，△ABP为等腰三角形．

点评 此题是四边形综合题，主要考查了平行四边形的性质，含30°的直角三角形的性质，等腰三角形的性质，解（1）的关键是求出梯形的高，解（2）的关键是利用AQ=BP建立方程，解（3）的关键是分类讨论的思想思考问题，是一道中考常考题．