题目内容
设a，b，c，d都是正数．求证：| a2+c2+d2+2cd |
| b2+c2 |
| a2+b2+d2+2ab |
分析：构建一个三角形使得其三边为：
+
＞
的三角形，根据三角形两边之和大于第三边可以求证．
| a2+c2+d2+2cd |
| b2+c2 |
| a2+b2+d2+2ab |
解答：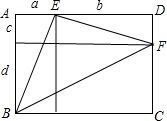
解：如图，构造一个边长为（a+b）、（c+d）的矩形ABCD，
在Rt△ABE中，BE=
，
所以BE=
=
在Rt△BCF中，BF=
=
=
在Rt△DEF中，EF=
=
在△BEF中，BE+EF＞BF
即
+
＞
．
解：如图，构造一个边长为（a+b）、（c+d）的矩形ABCD，在Rt△ABE中，BE=
| AE2+AB2 |
所以BE=
| a2+(c+d)2 |
| a2+c2+d2+2cd |
在Rt△BCF中，BF=
| BC2+CF2 |
| (a+b)2+d2 |
| a2+b2+d2+2ab |
在Rt△DEF中，EF=
| DE2+DF2 |
| b2+c2 |
在△BEF中，BE+EF＞BF
即
| a2+c2+d2+2cd |
| b2+c2 |
| a2+b2+d2+2ab |
点评：本题考查了勾股定理的运用，本题中设计矩形ABCD并且构建三角形BEF是解题的关键．
练习册系列答案
第三学期赢在暑假系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
相关题目
