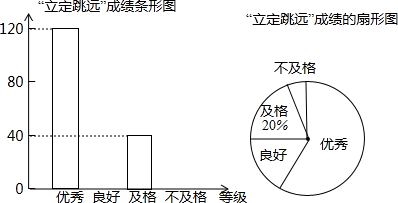
题目内容

2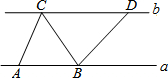．如图，直线a∥b，点A、B位于直线a上，点C、D位于直线b上，且AB：CD=2：3，如果△ABC的面积为6，那么△BCD的面积为9．

分析 根据两平行线间的距离处处相等，结合三角形的面积公式，知△BCD和△ABC的面积比等于CD：AB，从而进行计算．

解答 解：∵a∥b，
∴△BCD的面积：△ABC的面积=CD：AB=3：2，
∴△BCD的面积=6×$\frac{3}{2}$=9．
故答案为：9．

点评 此题考查了平行线间的距离以及三角形的面积比的一种方法，即等高的两个三角形的面积比等于它们的底的比．

练习册系列答案
相关题目
12．一个圆锥的底面半径为3，母线长为5，则圆锥的侧面积是（　　）
A．9πB．18πC．15πD．27π
13．某商场计划用5400元购买一批商品，若将进价降低10%，则可以多购买该商品30件．市场调查反映：售价为每件25元时，每天可卖出250件．如果调整价格，一件商品每涨价1元，每天要少卖出10件．
（1）求该商品原来的进价；
（2）在进价没有改变的条件下，若每天所得的销售利润2000元时，且销量尽可能大，商品的售价是多少元；
（3）在进价没有改变的条件下，商场的营销部在调控价格方面，提出了A，B两种营销方案．
方案A：每件商品涨价不超过5元；方案B：每件商品的利润至少为16元．
请比较哪种方案的最大利润更高，并说明理由．
10．化简：$\frac{1}{2}$（b-$\frac{k^2}{a^2b}$）（a-$\frac{k}{b}$）+$\frac{1}{2}$（b-$\frac{k^2}{a^2b}$）$\frac{k}{a}$．
17．养鱼专业户王老汉为方便与客户签订购销合同，对养鱼塘中的鱼进行评估，第一次捞出100条，称得质量为196kg，并将每条鱼作记号后放入水中，当它们完全混合于鱼群后，又捞出200条，称得质量为404kg，且带有记号的鱼有10条．王老汉的鱼塘中估计有鱼4000条，总质量为8000千克．
7．在Rt△ABC中，∠B=90°，AB=8，BC=6，将△ABC沿MN折叠（M、N分别在AC、AB上，且不与端点重合），使点A与BC上的点D重合，点D把线段BC分成长度之比是1：2的两条线段，则线段BN的长为（　　）
A．$\frac{15}{8}$B．3C．3或$\frac{15}{4}$D．$\frac{15}{4}$或4
14．若关于x、y的方程组$\left\{\begin{array}{l}{3x-ay=m}\\{x+my=n}\end{array}\right.$的解是$\left\{\begin{array}{l}{x=1}\\{y=1}\end{array}\right.$，则m-n的值是-1．
11．某区为了解八年级女生“立定跳远”试测情况，随机抽取了部分女生的测试成绩进行统计，根据评分标准，将她们的成绩分成“优秀”“良好”“及格”和“不及格”四个等级，并绘制出统计图的一部分（如图）

（1）在被调查的女生中，等级为“优秀”的有120人，“及格”等级对应的扇形圆心角的度数是72°
（2）在这次调查中，一共抽取了多少名女生的测试成绩？
（3）该区八年级共有2200名女生，试估计该区达到“优秀”等级的女生人数共有多少．
12．下列命题的逆命题正确的是（　　）
A．如果两个角是直角，那么它们相等B．全等三角形的面积相等
C．同位角相等，两直线平行D．若a=b，则a2=b2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网