题目内容
如图，在?ABCD中，AB=2BC，M为DC的中点，求∠AMB的度数．考点：平行四边形的性质
专题：
分析：可证明∠3=∠4，∠5=∠6，从而可得∠3+∠5=90°，也可得∠AMB的度数．
解答：解：如图所示：
∵四边形ABCD是平行四边形，AB=2BC，M为DC的中点，
∴DA=DM，CM=CB，
∴∠1=∠4，∠2=∠6，
又∵CD∥AB，
∴∠1=∠3，∠2=∠5，
∴∠3=∠4，∠5=∠6，
∵∠DAB+∠ABC=180°，
∴∠3+∠5=90°，
∴∠AMB=90°．
∵四边形ABCD是平行四边形，AB=2BC，M为DC的中点，
∴DA=DM，CM=CB，
∴∠1=∠4，∠2=∠6，
又∵CD∥AB，
∴∠1=∠3，∠2=∠5，
∴∠3=∠4，∠5=∠6，
∵∠DAB+∠ABC=180°，
∴∠3+∠5=90°，
∴∠AMB=90°．
点评：本题考查了平行四边形的性质，解答本题的关键是掌握平行四边形的对边平行且相等．
练习册系列答案
相关题目
如图，∠CPA=∠A+∠B+∠C成立吗？说明理由．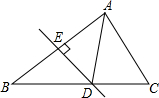
如图，在△ABC中，已知BC比AC长3cm，AB的垂直平分线交BC于点D，交AB于点E，△ACD的周长是15cm，求BC和AC的长．