题目内容
已知m是方程x2-2016x+1=0的一个不为0的根，求m2-2015m+
的值．
| 2016 |
| m2+1 |
考点：一元二次方程的解
专题：
分析：把x=m代入方程x2-2016x+1=0有m2-2016m+1=0，变形得m2-2015m=m-1，m2+1=2016m，再将所求代数式m2-2015m+
变形为
-1，将
=2016代入，计算即可求出结果．
| 2016 |
| m2+1 |
| m2+1 |
| m |
| m2+1 |
| m |
解答：解：∵m是方程x2-2016x+1=0的一个不为0的根，
∴m2-2016m+1=0，
∴m2-2015m=m-1，m2+1=2016m，
∴
=
=
，
∴m2-2015m+
=m-1+
=
-1=2016-1=2015．
∴m2-2016m+1=0，
∴m2-2015m=m-1，m2+1=2016m，
∴
| 2016 |
| m2+1 |
| 2016 |
| 2016m |
| 1 |
| m |
∴m2-2015m+
| 2016 |
| m2+1 |
| 1 |
| m |
| m2+1 |
| m |
点评：本题考查的是一元二次方程的解，把方程的解代入方程，得到关于m的式子，代入代数式化简求值．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
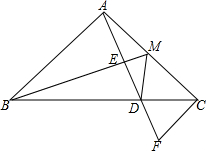已知如图，在△ABC中，∠BAC=90°，AB=AC，M是AC边的中点，AD⊥BM交BC于D，交BM于E，CF⊥AC，证明：
如图，菱形ABCD的对角线AC和BD相交于点O，求证：S菱形ABCD=