题目内容
定义:如图1,点M,N把线段AB分割成AM,MN和BN,若以AM,MN,BN为边的三角形是一个直角三角形,则称点M,N是线段AB的勾股分割点
(1)已知点M,N是线段AB的勾股分割点,若AM=2,MN=3求BN的长;
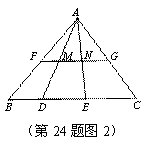
(2)如图2,在△ABC中,FG是中位线,点D,E是线段BC的勾股分割点,且EC>DE≥BD,连接AD,AE分别交FG于点M,N,求证:点M,N是线段FG的勾股分割点
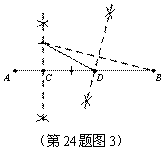
(3)已知点C是线段AB上的一定点,其位置如图3所示,请在BC上画一点D,使C,D是线段AB的勾股分割点(要求尺规作图,保留作图痕迹,画出一种情形即可)
(4)如图4,已知点M,N是线段AB的勾股分割点,MN>AM≥BN,△AMC,△MND
和△NBM均是等边三角形,AE分别交CM,DM,DN于点F,G,H,若H是DN的中点,试探究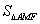 ,
,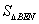 和
和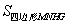 的数量关系,并说明理由21教育网
的数量关系,并说明理由21教育网
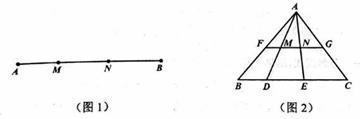

(1)解:当 为最大线段时,
为最大线段时,
 ∵点
∵点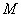 ,
,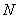 是线段
是线段 的勾股分割点,
的勾股分割点,
∴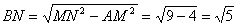 .
.
当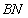 为最大线段时,
为最大线段时,
∵点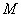 ,
,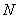 是线段
是线段 的勾股分割点,
的勾股分割点,
∴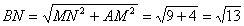 .
.
综上,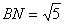 或
或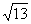 .
.
(2)证明:∵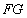 是△
是△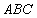 的中位线,∴
的中位线,∴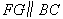 .
.
∴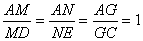 .
.
∴点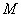 ,
,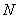 分别是
分别是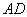 ,
,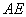 的中点.
的中点.
∴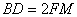 ,
,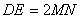 ,
,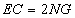 .
.  ∵点
∵点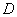 ,
,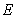 是线段
是线段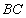 的勾股分割点,且
的勾股分割点,且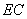 >
>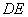 ≥
≥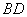 ,
,
∴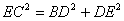 .
.
∴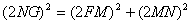 .
.
∴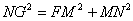 .
.
∴点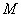 ,
,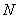 是线段
是线段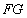 的勾股分割点.
的勾股分割点.
(3)用尺规画出图形,如图3所示.
(4)解: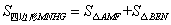 .
.
理由:设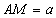 ,
,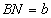 ,
,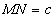 ,
,
∵ 是
是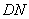 的中点,∴
的中点,∴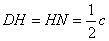 .
.
∵△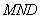 ,△
,△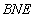 均为等边三角形,
均为等边三角形,
 ∴
∴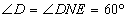 .
.
∵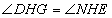 ,
,
∴△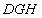 ≌△
≌△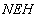 .
.
∴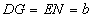 .∴
.∴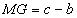 .
.
∵ ,∴△
,∴△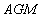 ∽△
∽△ .
.
∴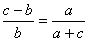 .
.
∴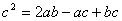 .
.
∵点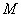 ,
,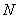 是线段
是线段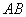 的勾股分割点,
的勾股分割点,
∴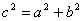 .
.
∴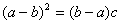 ,
,
又∵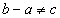 .∴
.∴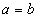 .
.
在△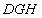 和△
和△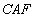 中,
中,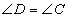 ,
,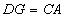 ,
,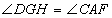 ,
,
∴△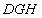 ≌△
≌△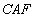 .
.
∴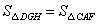 .
.
∵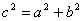 ,∴
,∴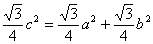 .
.
∴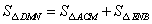 .
.
∵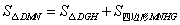 ,
,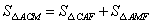 ,
,
∴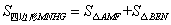 .
.

 的相反数是( )
的相反数是( )

 0.57,cos35°
0.57,cos35°
 的值为( )
的值为( )
