题目内容
15. 已知,如图,四边形ABCD中,AC=7,BD=8,E、F、G、H分别是AB、BC、CD、DA的中点,则四边形EFGH的周长=15.
已知,如图,四边形ABCD中,AC=7,BD=8,E、F、G、H分别是AB、BC、CD、DA的中点,则四边形EFGH的周长=15.
分析 根据三角形中位线定理分别求出EF+FG+GH+HE的长,根据四边形的周长公式计算即可.
解答 解:∵E、F、G、H分别是AB、BC、CD、DA的中点,
∴EF、FG、GH、HF分别是△ABC、△BCD、△CDA、△DAB的中位线,
∴EF=$\frac{1}{2}$AC=3.5,FG=$\frac{1}{2}$BD=4,GH=$\frac{1}{2}$AC=3.5,HE=$\frac{1}{2}$BD=4,
∴四边形EFGH的周长=EF+FG+GH+HE=15.,
故答案为:15.
点评 本题考查的是中点四边形的判定和性质,掌握三角形中位线定理是解题的关键.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
5.56.2万平方米用科学记数法表示正确的是( )
| A. | 5.62×104m2 | B. | 56.2×104m2 | C. | 5.62×105m2 | D. | 0.562×103m2 |
6.某天蔬菜经营户用120元批发了西兰花和胡萝卜共60kg到菜市场零售,西兰花和胡萝卜当天的批发价和零售价如表所示:
如果他当天全部卖完这些西兰花和胡萝卜可获得利润多少元.
| 品名 | 西兰花 | 胡萝卜 |
| 批发价(元/kg) | 2.8 | 1.6 |
| 零售价(元/kg) | 3.8 | 2.5 |
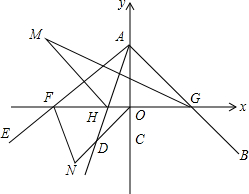 如图,平面直角坐标系中,∠BAC=45°,AC在y轴上,∠DAE=35°,AE,AB,AD分别交x轴于点F、G、H.在∠DAE旋转过程中,设AE交x轴于F,∠AGH的平分线与∠AHF的平分线交于点M,∠COF的平分线与∠OFE的平分线交于点N.下列两个结论:①∠N+∠M为定值;②∠N-∠M为定值.其中有且仅有一个是正确的,请你选出正确的结论,并求出其值.
如图,平面直角坐标系中,∠BAC=45°,AC在y轴上,∠DAE=35°,AE,AB,AD分别交x轴于点F、G、H.在∠DAE旋转过程中,设AE交x轴于F,∠AGH的平分线与∠AHF的平分线交于点M,∠COF的平分线与∠OFE的平分线交于点N.下列两个结论:①∠N+∠M为定值;②∠N-∠M为定值.其中有且仅有一个是正确的,请你选出正确的结论,并求出其值.