题目内容
3.求证:正方形的对角线相等且互相垂直平分.分析 首先写出已知,求证.然后根据平行四边形的性质即可证明.
解答 已知:如图四边形ABCD是正方形, 求证:AC=BD,AC⊥BD,OA=OC,OB=0D.
求证:AC=BD,AC⊥BD,OA=OC,OB=0D.
证明:∵四边形ABCD是正方形,
∴OB=OD,OA=OC(平行四边形对角线互相平分)
∵AB=AD,
∴AC⊥BD(三线合一),
∵∠BAD=90°,
∴AO=OD=OB=OC(直角三角形斜边中线等于斜边一半),
∴AC=BD,
∴正方形的对角线相等且互相垂直平分.
点评 本题考查正方形的性质的证明,解题的关键是只能用平行四边形的性质去证明,这是定理证明,属于基础题.

练习册系列答案
相关题目
12.有以下四种说法:
①过一点有且只有一条直线与已知直线垂直;
②过直线外一点有且只有一条直线与已知直线平行;
③平行于同一条直线的两条直线平行;
④垂直于同一条直线的两条直线垂直;
③直线外一点和直线上所有点的连线中,垂线段最短.
其中正确的有( )
①过一点有且只有一条直线与已知直线垂直;
②过直线外一点有且只有一条直线与已知直线平行;
③平行于同一条直线的两条直线平行;
④垂直于同一条直线的两条直线垂直;
③直线外一点和直线上所有点的连线中,垂线段最短.
其中正确的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
2. 如图,在△ABC中,AB=6,∠B=60°,以BC所在直线为x轴,以B点为原点建立直角坐标系,则点A的坐标是( )
如图,在△ABC中,AB=6,∠B=60°,以BC所在直线为x轴,以B点为原点建立直角坐标系,则点A的坐标是( )
 如图,在△ABC中,AB=6,∠B=60°,以BC所在直线为x轴,以B点为原点建立直角坐标系,则点A的坐标是( )
如图,在△ABC中,AB=6,∠B=60°,以BC所在直线为x轴,以B点为原点建立直角坐标系,则点A的坐标是( )| A. | (3,3) | B. | (3$\sqrt{3}$,3) | C. | (3,$3\sqrt{3}$) | D. | (3$\sqrt{3}$,3$\sqrt{3}$) |
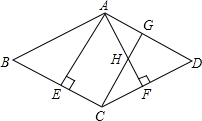 如图所示,菱形ABCD中,AB=4,E为BC中点,AE⊥BC,AF⊥CD,CG∥AE,CG交AF于点H,交AD于点G.
如图所示,菱形ABCD中,AB=4,E为BC中点,AE⊥BC,AF⊥CD,CG∥AE,CG交AF于点H,交AD于点G. 如图,在△ABC,AC=BC,且∠ACB=∠ADC=∠BEC=100°,求证:DE=AD+BE.
如图,在△ABC,AC=BC,且∠ACB=∠ADC=∠BEC=100°,求证:DE=AD+BE.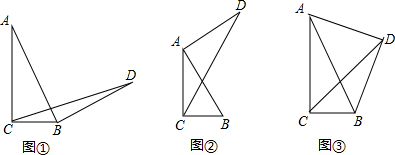
 已知,如图,四边形ABCD中,AC=7,BD=8,E、F、G、H分别是AB、BC、CD、DA的中点,则四边形EFGH的周长=15.
已知,如图,四边形ABCD中,AC=7,BD=8,E、F、G、H分别是AB、BC、CD、DA的中点,则四边形EFGH的周长=15.