ЬтФПФкШн
ЁОЬтФПЁПдФЖСЯТУцВФСЯ:аЁДЯгіЕНетбљвЛИіЮЪЬт: ШчЭМ1ЃЌ![]() ЃЌЧыЛвЛИі
ЃЌЧыЛвЛИі![]() ЃЌЪЙ
ЃЌЪЙ![]() гы
гы![]() ЛЅВЙ.
ЛЅВЙ.

аЁДЯЪЧетбљЫМПМЕФ:ЪзЯШЭЈЙ§ЗжЮіУїШЗЩфЯп![]() дк
дк![]() ЕФЭтВПЃЌЛГіЪОвтЭМЃЌШчЭМ2ЫљЪО:ШЛКѓЭЈЙ§ЙЙдьЦННЧевЕН
ЕФЭтВПЃЌЛГіЪОвтЭМЃЌШчЭМ2ЫљЪО:ШЛКѓЭЈЙ§ЙЙдьЦННЧевЕН![]() ЕФВЙНЧ
ЕФВЙНЧ![]() ЃЌ
ЃЌ

ШчЭМ3ЫљЪО:НјЖјЗжЮівЊЪЙ![]() гы
гы![]() ЛЅВЙЃЌдђаш
ЛЅВЙЃЌдђаш![]() .
.

вђДЫЃЌаЁДЯевЕНСЫНтОіЮЪЬтЕФЗНЗЈ:ЗДЯђбгГЄЩфЯп![]() ЕУЕНЩфЯп
ЕУЕНЩфЯп![]() ЃЌРћгУСПНЧЦїЛГі
ЃЌРћгУСПНЧЦїЛГі![]() ЕФЦНЗжЯп
ЕФЦНЗжЯп![]() ЃЌетбљОЭЕУЕНСЫ
ЃЌетбљОЭЕУЕНСЫ![]() гы
гы![]() ЛЅВЙ
ЛЅВЙ
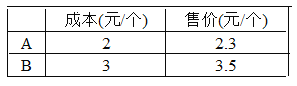
(1)аЁДЯИљОнздМКЕФЛЗЈаДГіСЫМКжЊКЭЧѓжЄЃЌЧыФуЭъГЩжЄУї.вбжЊ:ШчЭМ3ЃЌЕу![]() дкжБЯп
дкжБЯп![]() ЩЯЃЌЩфЯп
ЩЯЃЌЩфЯп![]() ЦНЗж
ЦНЗж![]() .ЧѓжЄ:
.ЧѓжЄ: ![]() гы
гы![]() ЛЅВЙ. .
ЛЅВЙ. .

(2)ВЮПМаЁДЯЕФЛЗЈЃЌЧыдкЯТЭМжаЛГі--Иі![]() ЃЌЪЙ
ЃЌЪЙ![]() гы
гы![]() ЛЅгр.(БЃСєЛЭМКлМЃ)
ЛЅгр.(БЃСєЛЭМКлМЃ)

(3)вбжЊ![]() КЭ
КЭ![]() ЛЅгрЃЌЩфЯп
ЛЅгрЃЌЩфЯп![]() ЦНЗж
ЦНЗж![]() ЃЌЩфЯп
ЃЌЩфЯп![]() ЦНЗж
ЦНЗж![]() .Шє
.Шє![]() ЃЌжБНгаДГіШёНЧ
ЃЌжБНгаДГіШёНЧ![]() ЕФЖШЪ§ЪЧ .
ЕФЖШЪ§ЪЧ .
ЁОД№АИЁПЃЈ1ЃЉМћНтЮіЃЛЃЈ2ЃЉМћНтЮіЃЛЃЈ3ЃЉ![]() Лђ
Лђ![]()
ЁОНтЮіЁП
(1)ИљОнСкВЙНЧЕФЖЈвхЕУГі![]() ЃЌдйИљОнНЧЦНЗжЯпЕФЖЈвхПЩЕУ
ЃЌдйИљОнНЧЦНЗжЯпЕФЖЈвхПЩЕУ![]() ЃЌДгЖјЕУГі
ЃЌДгЖјЕУГі![]() гы
гы![]() ЛЅВЙ.
ЛЅВЙ.
(2)ЯШЙЙдьжБНЧЃЌЛ![]() Лђ
Лђ![]() ЃЌдйРћгУСПНЧЦїЛГі
ЃЌдйРћгУСПНЧЦїЛГі![]() Лђ
Лђ![]() ЕФЦНЗжЯп
ЕФЦНЗжЯп![]() ЃЌМДПЩЕУГі
ЃЌМДПЩЕУГі![]() гы
гы![]() ЛЅгр
ЛЅгр
(3)ЯШЗжPFдкPQЕФгвВрКЭзѓВрЃЌЛГіЭМаЮЃЌдйИљОнНЧЦНЗжЯпЕФаджЪКЭНЧЕФКЭВюМДПЩЕУГіНсТл
НтЃК(1)жЄУї:![]() Еу
Еу![]() дкжБЯп
дкжБЯп![]() ЩЯЃЌ
ЩЯЃЌ
![]() .
.
МД![]() .
.
![]() .
.
![]() ЦНЗж
ЦНЗж![]() ЃЌ
ЃЌ
![]() .
.
![]()
![]() гы
гы![]() ЛЅВЙ.
ЛЅВЙ.
(2) Л![]() Лђ
Лђ![]() ЃЌдйЗжБ№ЛГі
ЃЌдйЗжБ№ЛГі![]() Лђ
Лђ![]() ЕФЦНЗжЯп
ЕФЦНЗжЯп![]()
ШчЭМЫљЪО
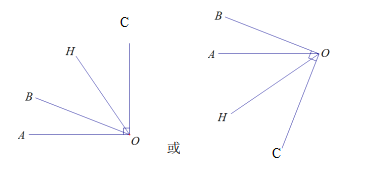
(3) ЕБPFдкPQЕФгвВрЪБЃЌИљОнЬтвтЛГіЭМаЮШчЭМ
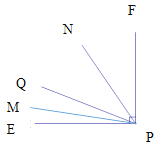
ЁпЩфЯп![]() ЦНЗж
ЦНЗж![]() ЃЌЩфЯп
ЃЌЩфЯп![]() ЦНЗж
ЦНЗж![]() .
.
Ёр![]() ЃЌ
ЃЌ![]()
Ёр![]()
Ёп![]() КЭ
КЭ![]() ЛЅгрЃЌ
ЛЅгрЃЌ
Ёр![]()
Ёр![]()
ЕБPFдкPQЕФгвВрЪБЃЌИљОнЬтвтЛГіЭМаЮ
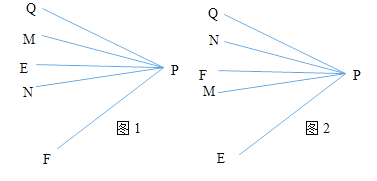
ШчЭМ1ЃКЁпЩфЯпPMЦНЗж![]() ЃЌЩфЯп
ЃЌЩфЯп![]() ЦНЗж
ЦНЗж![]() .
.
Ёр![]() ЃЌ
ЃЌ![]()
Ёр![]()
Ёп![]() КЭ
КЭ![]() ЛЅгрЃЌ
ЛЅгрЃЌ![]()
Ёр![]()
Ёр![]()
ШчЭМ2ЁпPMЦНЗж![]() ЃЌЩфЯп
ЃЌЩфЯп![]() ЦНЗж
ЦНЗж![]() .
.
Ёр![]() ЃЌ
ЃЌ![]()
Ёр![]()
Ёп![]() КЭ
КЭ![]() ЛЅгрЃЌ
ЛЅгрЃЌ![]()
Ёр![]()
Ёр![]()
злЩЯЫљЪіПЩЕУЃК![]() =45ЁуЛђ
=45ЁуЛђ![]()
ЙЪД№АИЮЊЃК45ЁуЛђ![]()

 УћаЃПЮЬУЯЕСаД№АИ
УћаЃПЮЬУЯЕСаД№АИ