ĖâÄŋÄÚČÝ
ĄūĖâÄŋĄŋĢĻ2016šÚÁú―ĘĄđþķûąõĘÐĢĐŌŅÖŠĢšĄũABCÄÚ―ÓÓÚĄŅOĢŽDĘĮ![]() ÉÏŌŧĩãĢŽODĄÍBCĢŽīđŨãΊHĢŪ
ÉÏŌŧĩãĢŽODĄÍBCĢŽīđŨãΊHĢŪ
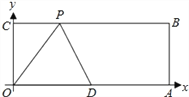
ĢĻ1ĢĐČįÍž1ĢŽĩąÔēÐÄOÔÚABąßÉÏĘąĢŽĮóÖĪĢšAC=2OHĢŧ
ĢĻ2ĢĐČįÍž2ĢŽĩąÔēÐÄOÔÚĄũABCÍâēŋĘąĢŽÁŽ―ÓADĄĒCDĢŽADÓëBC―ŧÓÚĩãPĢŽĮóÖĪĢšĄÏACD=ĄÏAPBĢŧ
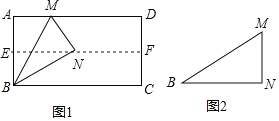
ĢĻ3ĢĐÔÚĢĻ2ĢĐĩÄĖõžþÏÂĢŽČįÍž3ĢŽÁŽ―ÓBDĢŽEΊĄŅOÉÏŌŧĩãĢŽÁŽ―ÓDE―ŧBCÓÚĩãQĄĒ―ŧABÓÚĩãNĢŽÁŽ―ÓOEĢŽBFΊĄŅOĩÄÏŌĢŽBFĄÍOEÓÚĩãR―ŧDEÓÚĩãGĢŽČôĄÏACDĐĄÏABD=2ĄÏBDNĢŽAC=![]() ĢŽBN=
ĢŽBN=![]() ĢŽtanĄÏABC=
ĢŽtanĄÏABC=![]() ĢŽĮóBFĩÄģĪĢŪ
ĢŽĮóBFĩÄģĪĢŪ

Ąūīð°ļĄŋĢĻ1ĢĐÖĪÃũžû―âÎöĢŧĢĻ2ĢĐÖĪÃũžû―âÎöĢŧĢĻ3ĢĐ24ĢŪ
Ąū―âÎöĄŋĘÔĖâ·ÖÎöĢšĢĻ1ĢĐODĄÍBCŋÉÖŠĩãHĘĮBCĩÄÖÐĩãĢŽÓÖÖÐÎŧÏßĩÄÐÔÖĘŋÉĩÃAC=2OHĢŧ
ĢĻ2ĢĐÓÉīđūķķĻĀíŋÉÖŠĢš![]() ĢŽËųŌÔĄÏBAD=ĄÏCADĢŽÓÉŌōΊĄÏABC=ĄÏADCĢŽËųŌÔĄÏACD=ĄÏAPBĢŧ
ĢŽËųŌÔĄÏBAD=ĄÏCADĢŽÓÉŌōΊĄÏABC=ĄÏADCĢŽËųŌÔĄÏACD=ĄÏAPBĢŧ
ĢĻ3ĢĐÓÉĄÏACDĐĄÏABD=2ĄÏBDNŋÉÖŠĄÏAND=90ĄãĢŽÓÉtanĄÏABC=![]() ŋÉÖŠNQšÍBQĩÄģĪķČĢŽÔŲÓÉBFĄÍOEšÍODĄÍBCŋÉÖŠĄÏGBN=ĄÏABCĢŽËųŌÔBG=BQĢŽÁŽ―ÓAOēĒŅÓģĪ―ŧĄŅOÓÚĩãIĢŽÁŽ―ÓICšóĀûÓÃÔēÖÜ―ĮķĻĀíŋÉĮóĩÃICšÍAIĩÄģĪķČĢŽÉčQH=xĢŽĀûÓÃđīđÉķĻĀíŋÉĮóģöQHšÍHDĩÄģĪķČĢŽĀûÓÃīđūķķĻĀíŋÉĮóĩÃEDĩÄģĪķČĢŽŨîšóĀûÓÃtanĄÏOED=
ŋÉÖŠNQšÍBQĩÄģĪķČĢŽÔŲÓÉBFĄÍOEšÍODĄÍBCŋÉÖŠĄÏGBN=ĄÏABCĢŽËųŌÔBG=BQĢŽÁŽ―ÓAOēĒŅÓģĪ―ŧĄŅOÓÚĩãIĢŽÁŽ―ÓICšóĀûÓÃÔēÖÜ―ĮķĻĀíŋÉĮóĩÃICšÍAIĩÄģĪķČĢŽÉčQH=xĢŽĀûÓÃđīđÉķĻĀíŋÉĮóģöQHšÍHDĩÄģĪķČĢŽĀûÓÃīđūķķĻĀíŋÉĮóĩÃEDĩÄģĪķČĢŽŨîšóĀûÓÃtanĄÏOED=![]() žīŋÉĮóĩÃRGĩÄģĪķČĢŽŨîšóÓÉīđūķķĻĀíŋÉĮóĩÃBFĩÄģĪķČĢŪ
žīŋÉĮóĩÃRGĩÄģĪķČĢŽŨîšóÓÉīđūķķĻĀíŋÉĮóĩÃBFĩÄģĪķČĢŪ
ĘÔĖâ―âÎöĢšĢĻ1ĢĐĄßODĄÍBCĢŽĄāÓÉīđūķķĻĀíŋÉÖŠĢšĩãHĘĮBCĩÄÖÐĩãĢŽĄßĩãOĘĮABĩÄÖÐĩãĢŽĄāOHĘĮĄũABCĩÄÖÐÎŧÏßĢŽĄāAC=2OHĢŧ
ĢĻ2ĢĐĄßODĄÍBCĢŽĄāÓÉīđūķķĻĀíŋÉÖŠĢš![]() ĢŽĄāĄÏBAD=ĄÏCADĢŽĄß
ĢŽĄāĄÏBAD=ĄÏCADĢŽĄß![]() ĢŽĄāĄÏABC=ĄÏADCĢŽĄā180ĄãĐĄÏBADĐĄÏABC=180ĄãĐĄÏCADĐĄÏADCĢŽĄāĄÏACD=ĄÏAPBĢŽĢĻ3ĢĐÁŽ―ÓAOŅÓģĪ―ŧÓÚĄŅOÓÚĩãIĢŽÁŽ―ÓICĢŽABÓëODÏā―ŧÓÚĩãMĢŽĄßĄÏACDĐĄÏABD=2ĄÏBDNĢŽĄāĄÏACDĐĄÏBDN=ĄÏABD+ĄÏBDNĢŽĄßĄÏABD+ĄÏBDN=ĄÏANDĢŽĄāĄÏACDĐĄÏBDN=ĄÏANDĢŽĄßĄÏACD+ĄÏABD=180ĄãĢŽĄāĄÏABD+ĄÏBDN=180ĄãĐĄÏANDĢŽĄāĄÏAND=180ĄãĐĄÏANDĢŽĄāĄÏAND=90ĄãĢŽĄßtanĄÏABC=
ĢŽĄāĄÏABC=ĄÏADCĢŽĄā180ĄãĐĄÏBADĐĄÏABC=180ĄãĐĄÏCADĐĄÏADCĢŽĄāĄÏACD=ĄÏAPBĢŽĢĻ3ĢĐÁŽ―ÓAOŅÓģĪ―ŧÓÚĄŅOÓÚĩãIĢŽÁŽ―ÓICĢŽABÓëODÏā―ŧÓÚĩãMĢŽĄßĄÏACDĐĄÏABD=2ĄÏBDNĢŽĄāĄÏACDĐĄÏBDN=ĄÏABD+ĄÏBDNĢŽĄßĄÏABD+ĄÏBDN=ĄÏANDĢŽĄāĄÏACDĐĄÏBDN=ĄÏANDĢŽĄßĄÏACD+ĄÏABD=180ĄãĢŽĄāĄÏABD+ĄÏBDN=180ĄãĐĄÏANDĢŽĄāĄÏAND=180ĄãĐĄÏANDĢŽĄāĄÏAND=90ĄãĢŽĄßtanĄÏABC=![]() ĢŽBN=
ĢŽBN=![]() ĢŽĄāNQ=
ĢŽĄāNQ=![]() ĢŽĄāÓÉđīđÉķĻĀíŋÉĮóĩÃĢšBQ=
ĢŽĄāÓÉđīđÉķĻĀíŋÉĮóĩÃĢšBQ=![]() ĢŽĄßĄÏBNQ=ĄÏQHD=90ĄãĢŽĄāĄÏABC=ĄÏQDHĢŽĄßOE=ODĢŽĄāĄÏOED=ĄÏQDHĢŽĄßĄÏERG=90ĄãĢŽĄāĄÏOED=ĄÏGBNĢŽĄāĄÏGBN=ĄÏABCĢŽĄßABĄÍEDĢŽĄāBG=BQ=
ĢŽĄßĄÏBNQ=ĄÏQHD=90ĄãĢŽĄāĄÏABC=ĄÏQDHĢŽĄßOE=ODĢŽĄāĄÏOED=ĄÏQDHĢŽĄßĄÏERG=90ĄãĢŽĄāĄÏOED=ĄÏGBNĢŽĄāĄÏGBN=ĄÏABCĢŽĄßABĄÍEDĢŽĄāBG=BQ=![]() ĢŽGN=NQ=
ĢŽGN=NQ=![]() ĢŽĄßAIĘĮĄŅOÖąūķĢŽĄāĄÏACI=90ĄãĢŽĄßtanĄÏAIC=tanĄÏABC=
ĢŽĄßAIĘĮĄŅOÖąūķĢŽĄāĄÏACI=90ĄãĢŽĄßtanĄÏAIC=tanĄÏABC=![]() ĢŽĄā
ĢŽĄā![]() =
=![]() ĢŽĄāIC=
ĢŽĄāIC=![]() ĢŽĄāÓÉđīđÉķĻĀíŋÉĮóĩÃĢšAI=25ĢŽÁŽ―ÓOBĢŽÉčQH=xĢŽĄßtanĄÏABC=tanĄÏODE=
ĢŽĄāÓÉđīđÉķĻĀíŋÉĮóĩÃĢšAI=25ĢŽÁŽ―ÓOBĢŽÉčQH=xĢŽĄßtanĄÏABC=tanĄÏODE=![]() ĢŽĄā
ĢŽĄā![]() =
=![]() ĢŽĄāHD=2xĢŽĄāOH=ODĐHD=
ĢŽĄāHD=2xĢŽĄāOH=ODĐHD=![]() Đ2xĢŽBH=BQ+QH=
Đ2xĢŽBH=BQ+QH=![]() +xĢŽÓÉđīđÉķĻĀíŋÉĩÃĢš
+xĢŽÓÉđīđÉķĻĀíŋÉĩÃĢš![]() ĢŽĄā
ĢŽĄā![]() ĢŽ―âĩÃĢšx=
ĢŽ―âĩÃĢšx=![]() ŧōx=
ŧōx=![]() ĢŪ
ĢŪ
ĒŲĩąQH=![]() ĘąĢŽĄāQD=
ĘąĢŽĄāQD=![]() QH=
QH=![]() ĢŽĄāND=QD+NQ=
ĢŽĄāND=QD+NQ=![]() ĢŽĄāMN=
ĢŽĄāMN=![]() ĢŽMD=15ĢŪĄßMDĢū
ĢŽMD=15ĢŪĄßMDĢū![]() ĢŽĄāQH=
ĢŽĄāQH=![]() ēŧ·ûšÏĖâŌâĢŽÉáČĨĢŧ
ēŧ·ûšÏĖâŌâĢŽÉáČĨĢŧ
ĒÚĩąQH=![]() ĘąĢŽĄāQD=
ĘąĢŽĄāQD=![]() QH=
QH=![]() ĢŽĄāND=NQ+QD=
ĢŽĄāND=NQ+QD=![]() ĢŽÓÉīđūķķĻĀíŋÉĮóĩÃĢšED=
ĢŽÓÉīđūķķĻĀíŋÉĮóĩÃĢšED=![]() ĢŽĄāGD=GN+ND=
ĢŽĄāGD=GN+ND=![]() ĢŽĄāEG=EDĐGD=
ĢŽĄāEG=EDĐGD=![]() ĢŽĄßtanĄÏOED=
ĢŽĄßtanĄÏOED=![]() ĢŽĄā
ĢŽĄā![]() =
=![]() ĢŽĄāEG=
ĢŽĄāEG=![]() RGĢŽĄāRG=
RGĢŽĄāRG=![]() ĢŽĄāBR=RG+BG=12ĢŽĄāÓÉīđūķķĻĀíŋÉÖŠĢšBF=2BR=24ĢŪ
ĢŽĄāBR=RG+BG=12ĢŽĄāÓÉīđūķķĻĀíŋÉÖŠĢšBF=2BR=24ĢŪ

 Ņ§ÆÚļīÏ°ŌŧąūÍĻŅ§Ï°ŨÜķŊÔąÆÚÄĐžÓĘîžŲŅÓąßČËÃņģö°æÉįÏĩÁÐīð°ļ
Ņ§ÆÚļīÏ°ŌŧąūÍĻŅ§Ï°ŨÜķŊÔąÆÚÄĐžÓĘîžŲŅÓąßČËÃņģö°æÉįÏĩÁÐīð°ļ ÃĒđû―ĖļĻĘîžŲĖėĩØÖØĮėģö°æÉįÏĩÁÐīð°ļ
ÃĒđû―ĖļĻĘîžŲĖėĩØÖØĮėģö°æÉįÏĩÁÐīð°ļĄūĖâÄŋĄŋĄ°ËŦĘŪŌŧĄąŌŅūģÉΊÖÐđúĩįŨÓÉĖÎņÐÐŌĩĩÄÄęķČĘĒĘÂĢŽÃŋÄęÕâŌŧĖėģÉΊČŦÃņĩÄđšÎï―ÚĢŪÔÚ―ņÄęĩÄĄ°ËŦĘŪ ŌŧĄąÆÚžäĢŽÄģÍøĩęūŲ°ėīŲÏúŧîķŊĢŽ·―°ļČįÏÂąíËųĘūĢš
ŌŧīÎÐÔđšÎï―ðķî | īŲÏú·―°ļ |
ĩÍÓÚ | ËųđšÉĖÆ·ČŦēŋ°īūÅÕÛ―áËã |
| ËųđšÉĖÆ·ČŦēŋ°ī°ËÕÛ―áËã |
| ÆäÖÐĮ° |
![]() ČįđûđËŋÍÔÚļÃÍøĩęŌŧīÎÐÔđšÎï
ČįđûđËŋÍÔÚļÃÍøĩęŌŧīÎÐÔđšÎï![]() ÔŠĢĻ
ÔŠĢĻ![]() ĢŽĮóĘĩžĘļķŋîķāÉŲÔŠĢŋĢĻÓÚŽ
ĢŽĮóĘĩžĘļķŋîķāÉŲÔŠĢŋĢĻÓÚŽ ![]() ĩÄīúĘýĘ―ąíĘūĢĐ
ĩÄīúĘýĘ―ąíĘūĢĐ
![]() ÄģđËŋÍÔÚļÃĩęÁ―īÎđšÎïĩÄÉĖÆ·đēžÆ
ÄģđËŋÍÔÚļÃĩęÁ―īÎđšÎïĩÄÉĖÆ·đēžÆ![]() ÔŠ.ČôĩÚŌŧīÎđšÎïÉĖÆ·ĩÄ―ðķîΊ
ÔŠ.ČôĩÚŌŧīÎđšÎïÉĖÆ·ĩÄ―ðķîΊ ![]() ÔŠ(
ÔŠ(![]() )ĢŽĮóļÃđËŋÍÁ―īÎđšÎïĩÄĘĩžĘļķŋîđēķāÉŲÔŠĢŋ(ÓÚŽ
)ĢŽĮóļÃđËŋÍÁ―īÎđšÎïĩÄĘĩžĘļķŋîđēķāÉŲÔŠĢŋ(ÓÚŽ![]() ĩÄīúĘýĘ―ąíĘū)
ĩÄīúĘýĘ―ąíĘū)