题目内容
 如图,已知抛物线y=x2+bx+c与x轴交于A,B两点(点A在点B的左侧)与y轴交于点C(0,-3),对称轴是直线x=1,直线BC与抛物线的对称轴交于点D,点E为y轴上一动点,CE的垂直平分线交抛物线于P,Q两点(点P在第三象限)
如图,已知抛物线y=x2+bx+c与x轴交于A,B两点(点A在点B的左侧)与y轴交于点C(0,-3),对称轴是直线x=1,直线BC与抛物线的对称轴交于点D,点E为y轴上一动点,CE的垂直平分线交抛物线于P,Q两点(点P在第三象限)(1)求抛物线的函数表达式和直线BC的函数表达式;
(2)当△CDE是直角三角形,且∠CDE=90° 时,求出点P的坐标;
(3)当△PBC的面积为
| 21 |
| 8 |
考点:二次函数综合题
专题:
分析:(1)用对称轴公式即可得出b的值,再利用抛物线与y轴交于点C(0,-3),求出抛物线解析式即可;由抛物线的解析式可求出B的坐标,进而可求出线BC的函数表达式;
(2)当∠CDE=90°时,则CE为斜边,则DG2=CG•GE,即1=(OC-OG)•(2-a),求出a的值,进而得出P点坐标;
(3)当△PBC的面积为
时,过P作PK∥x 轴,交直线BC于点K,设P(m,n),则n=m2-2m-3,由已知条件可得:S△PBC=S△PKC+S△PKB=
,进而可求出P的坐标,又因为点P在CE垂直平分线上,所以E的坐标可求出.
(2)当∠CDE=90°时,则CE为斜边,则DG2=CG•GE,即1=(OC-OG)•(2-a),求出a的值,进而得出P点坐标;
(3)当△PBC的面积为
| 21 |
| 8 |
| 21 |
| 8 |
解答:解:(1)∵抛物线的对称轴为直线x=1,
∴-
-=1,
∴b=-2
∵抛物线与y轴交于点C(0,-3),
∴c=-3,
∴抛物线的函数表达式为:y=x2-2x-3;
∵抛物线与x轴交于A、B两点,
当y=0时,x2-2x-3=0.
∴x1=-1,x2=3.
∵A点在B点左侧,
∴A(-1,0),B(3,0)
设过点B(3,0)、C(0,-3)的直线的函数表达式为y=kx+m,
则
,
∴
∴直线BC的函数表达式为y=x-3;
(2)∵Rt△CDE 中∠CDE=90°,直线BC的解析式为y=x-3,
∴∠OCB=45°,
∵点D在对称轴x=1与直线y=x-3交点上,
∴D坐标为(1,-2 )
Rt△CDE为等腰直角三角形易得E的坐标(0,-1),
∵点P在CE垂直平分线上,
∴点P纵坐标为-2,
∵点P在y=x2-2x-3上,
∴x2-2x-3=-2,
解得:x=1±
,
∵P在第三象限,
∴P的坐标为(1-
,-2);
(3)过P作PK∥x轴,交直线BC于点K,设P(m,n),则n=m2-2m-3
∵直线BC的解析式为y=x-3,
∴K的坐标为(n+3,n),
∴PK=n+3-m=m2-3m,
∵S△PBC=S△PKC+S△PKB=
,
∴
×3KP=
∴m2-3m=
,
解得:m=-
或
,
∵P在第三象限,
∴P的坐标为(-
,-
)
∵点P在CE垂直平分线上,
∴E的坐标为(0,-
)
∴-
| b |
| 2a |
∴b=-2
∵抛物线与y轴交于点C(0,-3),
∴c=-3,
∴抛物线的函数表达式为:y=x2-2x-3;
∵抛物线与x轴交于A、B两点,
当y=0时,x2-2x-3=0.
∴x1=-1,x2=3.
∵A点在B点左侧,
∴A(-1,0),B(3,0)
设过点B(3,0)、C(0,-3)的直线的函数表达式为y=kx+m,
则
|
∴
|
∴直线BC的函数表达式为y=x-3;
(2)∵Rt△CDE 中∠CDE=90°,直线BC的解析式为y=x-3,
∴∠OCB=45°,

∵点D在对称轴x=1与直线y=x-3交点上,
∴D坐标为(1,-2 )
Rt△CDE为等腰直角三角形易得E的坐标(0,-1),
∵点P在CE垂直平分线上,
∴点P纵坐标为-2,
∵点P在y=x2-2x-3上,
∴x2-2x-3=-2,
解得:x=1±
| 2 |
∵P在第三象限,
∴P的坐标为(1-
| 2 |
(3)过P作PK∥x轴,交直线BC于点K,设P(m,n),则n=m2-2m-3
∵直线BC的解析式为y=x-3,
∴K的坐标为(n+3,n),
∴PK=n+3-m=m2-3m,
∵S△PBC=S△PKC+S△PKB=
| 21 |
| 8 |
∴
| 1 |
| 2 |
| 21 |
| 8 |
∴m2-3m=
| 7 |
| 4 |
解得:m=-
| 1 |
| 2 |
| 7 |
| 2 |
∵P在第三象限,
∴P的坐标为(-
| 1 |
| 2 |
| 7 |
| 4 |
∵点P在CE垂直平分线上,
∴E的坐标为(0,-
| 1 |
| 2 |
点评:本题是二次函数的综合题型,其中涉及到的知识点有抛物线的顶点公式和三角形的面积求法以及用待定系数法求一次函数的解析式和等腰直角三角形的性质,在求有关动点问题时要注意分析题意分情况讨论结果.

练习册系列答案
相关题目
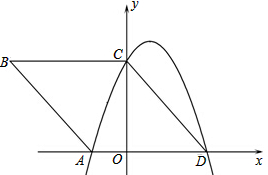 如图,在直角坐标系中,菱形ABCD的顶点A、C、D在坐标轴上,二次函数
如图,在直角坐标系中,菱形ABCD的顶点A、C、D在坐标轴上,二次函数
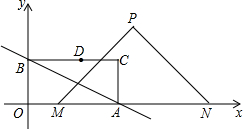 如图,在平面直角坐标系中,直线
如图,在平面直角坐标系中,直线 已知△ABC在网格中的位置如图,那么△ABC对应的圆心坐标是
已知△ABC在网格中的位置如图,那么△ABC对应的圆心坐标是