题目内容
已知:B,C是线段AD上的两点,且AB=CD.分别为AB,BC,CD,AD为直径作四个半圆,得到一个如图所示的轴对称图形.此图的对称轴分别交其中两个半圆于M,N交AD于O.若AD=16,AB=2r(0<r<4),回答下列问题:(1)用含r的代数式表示BC=
(2)设以MN为直径的圆的面积为S,阴影部分的面积为S阴影,请通过计算填写下表:
| r | S | S阴影 |
| r=1 | 49π | |
| r=2 | 36π | |
| r=3 | 25π |
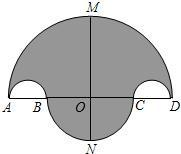
分析:(1)根据线段的和差关系可知:BC=16-4r,即OC=
BC=8-2r=ON,OM=AB+OB=2r+8-2r=8,所以MN=ON+OM=8-2r+8=16-2r.
(2)根据圆的面积公式进行计算,可得出S=S阴影,依此填写表格.
(3)利用面积公式证明.
| 1 |
| 2 |
(2)根据圆的面积公式进行计算,可得出S=S阴影,依此填写表格.
(3)利用面积公式证明.
解答:解:(1)16-4r,16-2r.(2分)
(2)如图所示:
(3)S=S阴影.
证明:∵S=π(
)2=π(8-r)2=64π-16πr+πr2
S阴影=
×82π-πr2+
π(8-2r)2=64π-16πr+πr2,
∴S=S阴影.(8分)
说明:证明中S阴影,S求对一个可得(1).结果写为π(8-r)2或其它形式不扣分.
(2)如图所示:
| r | S | S阴影 |
| r=1 | 49π | 49π |
| r=2 | 36π | 36π |
| r=3 | 25π | 25π |
证明:∵S=π(
| 16-2r |
| 2 |
S阴影=
| 1 |
| 2 |
| 1 |
| 2 |
∴S=S阴影.(8分)
说明:证明中S阴影,S求对一个可得(1).结果写为π(8-r)2或其它形式不扣分.
点评:本题主要考查了看图的能力,利用图中的线段关系和轴对称的性质,求出各圆的半径,然后再进行圆面积的计算.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
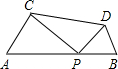 如图,已知AB=10,P是线段AB上任意一点,在AB的同侧分别以AP和PB为边作两个等边三角形APC和BPD,则线段CD的长度的最小值是( )
如图,已知AB=10,P是线段AB上任意一点,在AB的同侧分别以AP和PB为边作两个等边三角形APC和BPD,则线段CD的长度的最小值是( )| A、4 | ||
| B、5 | ||
| C、6 | ||
D、5(
|

 线段AB上的动点(不与端点重合),点O到EF,MN的距离分别为h1,h2,△OEF与△OGH组成的图形称为蝶形.
线段AB上的动点(不与端点重合),点O到EF,MN的距离分别为h1,h2,△OEF与△OGH组成的图形称为蝶形. 如图,已知点C、D是线段AB上两点,D是AC的中点,若CB=4cm,DB=7cm,求线段AB的长.
如图,已知点C、D是线段AB上两点,D是AC的中点,若CB=4cm,DB=7cm,求线段AB的长.