题目内容
图形既关于点O中心对称，又关于直线AC，BD对称，AC=10，BD=6，已知点E，M是
线段AB上的动点（不与端点重合），点O到EF，MN的距离分别为h1，h2，△OEF与△OGH组成的图形称为蝶形．（1）求蝶形面积S的最大值；
（2）当以EH为直径的圆与以MQ为直径的圆重合时，求h1与h2满足的关系式，并求h1的取值范围．
分析：（1）由题意，得四边形ABCD是菱形，根据EF∥BD，求证△ABD∽△AEF，然后利用其对边成比例求得EF，然后利用三角形面积公式即可求得蝶形面积S的最大值．
（2）根据题意，得OE=OM．作OR⊥AB于R，OB关于OR对称线段为OS，①当点E，M不重合时，则OE，OM在OR的两侧，可知RE=RM．利用勾股定理求得BR，由ML∥EK∥OB，利用平行线分线段求得
+
=
即可知h1的取值范围；②当点E，M重合时，则h1=h2，此时可知h1的取值范围．
（2）根据题意，得OE=OM．作OR⊥AB于R，OB关于OR对称线段为OS，①当点E，M不重合时，则OE，OM在OR的两侧，可知RE=RM．利用勾股定理求得BR，由ML∥EK∥OB，利用平行线分线段求得
| h1 |
| 5 |
| h2 |
| 5 |
| 9 |
| 17 |
解答：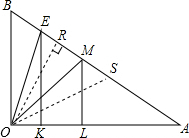
解：（1）由题意，得四边形ABCD是菱形．
∵EF∥BD，
∴△ABD∽△AEF，
∴
=
，即EF=
(5-h1)
∴S=2S△OEF=EF×h1=
(5-h1)×h1=-
(h1-
)2+
所以当h1=
时，Smax=
．
（2）根据题意，得OE=OM．
如图，作OR⊥AB于R，OB关于OR对称线段为OS，
①当点E，M不重合时，则OE，OM在OR的两侧，易知RE=RM．
∵AB=
=
，
∴OR=
，
∴BR=
=
由ML∥EK∥OB，
得
=
，
=
∴
+
=
+
=
，
即
+
=
∴h1+h2=
，此时h1的取值范围为0＜h1＜
且h1≠
，
②当点E，M重合时，则h1=h2，此时h1的取值范围为0＜h1＜5．
解：（1）由题意，得四边形ABCD是菱形．∵EF∥BD，
∴△ABD∽△AEF，
∴
| EF |
| 6 |
| 5-h1 |
| 5 |
| 6 |
| 5 |
∴S=2S△OEF=EF×h1=
| 6 |
| 5 |
| 6 |
| 5 |
| 5 |
| 2 |
| 15 |
| 2 |
所以当h1=
| 5 |
| 2 |
| 15 |
| 2 |
（2）根据题意，得OE=OM．
如图，作OR⊥AB于R，OB关于OR对称线段为OS，
①当点E，M不重合时，则OE，OM在OR的两侧，易知RE=RM．
∵AB=
| 52+32 |
| 34 |
∴OR=
| 15 | ||
|
∴BR=
32-(
|
| 9 | ||
|
由ML∥EK∥OB，
得
| OK |
| OA |
| BE |
| AB |
| OL |
| OA |
| BM |
| AB |
| OK |
| OA |
| OL |
| OA |
| BE |
| AB |
| BM |
| AB |
| 2BR |
| AB |
即
| h1 |
| 5 |
| h2 |
| 5 |
| 9 |
| 17 |
∴h1+h2=
| 45 |
| 17 |
| 45 |
| 17 |
| 45 |
| 34 |
②当点E，M重合时，则h1=h2，此时h1的取值范围为0＜h1＜5．
点评：此题主要考查相似三角形的判定与性质，勾股定理，菱形的判定与性质，轴对称的性质，中心对称，平行线分线段成比例等知识点，综合性强，有一定的拔高难度，属于难题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
，
，△OEF与△OGH组成的图形称为蝶形。
，
，△OEF与△OGH组成的图形称为蝶形。
，
，△OEF与△OGH组成的图形称为蝶形。
，
，△OEF与△OGH组成的图形称为蝶形。