题目内容
如图,Rt△ABC的直角边BC在x轴正半轴上,点D为斜边AC的中点,DB的延长线交y轴负半轴于点E,反比例函数 的图象经过点A.若S△BEC=4,则k的值为 ;
的图象经过点A.若S△BEC=4,则k的值为 ;
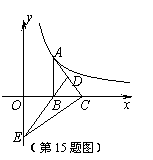
8

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
题目内容
如图,Rt△ABC的直角边BC在x轴正半轴上,点D为斜边AC的中点,DB的延长线交y轴负半轴于点E,反比例函数 的图象经过点A.若S△BEC=4,则k的值为 ;
的图象经过点A.若S△BEC=4,则k的值为 ;
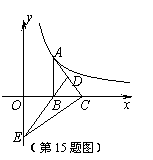
8

 阅读快车系列答案
阅读快车系列答案