题目内容
19.实践与探索(1)填空:$\sqrt{{3}^{2}}$=3;$\sqrt{(\frac{1}{2})^{2}}$=$\frac{1}{2}$; $\sqrt{{0}^{2}}$=0;$\sqrt{(-5)^{2}}$=5.
(2)观察第(1)题的计算结果回答:$\sqrt{{a}^{2}}$一定等于a吗?你发现其中的规律了吗?请把你观察到的规律归纳出来.
(3)利用你总结的规律计算:$\sqrt{(x-2)^{2}}$+$\sqrt{(x-3)^{2}}$,其中2<x<3.
分析 (1)根据二次根式的性质进行解答即可;
(2)根据(1)中的计算结果即可得出结论;
(3)根据(2)中的规律进行计算即可.
解答 解:(1)$\sqrt{{3}^{2}}$=3,$\sqrt{{(\frac{1}{2})}^{2}}$=$\frac{1}{2}$,$\sqrt{{0}^{2}}$=0,$\sqrt{{(-5)}^{2}}$=5.
故答案为:3,$\frac{1}{2}$,0,5;
(2)由(1)知,当a≥0时,$\sqrt{{a}^{2}}$=a;当a<0时,$\sqrt{{a}^{2}}$=-a.
(3)∵2<x<3,
∴x-2>0,x-3<0,
∴原式=x-2+(3-x)
=x-2+3-x
=1.
点评 本题考查的是二次根式的性质与化简,熟知二次根式具有非负性是解答此题的关键.

练习册系列答案
相关题目
9. 如图所示的空心几何体的俯视图是( )
如图所示的空心几何体的俯视图是( )
 如图所示的空心几何体的俯视图是( )
如图所示的空心几何体的俯视图是( )| A. |  | B. |  | C. |  | D. |  |
10.若(x-4)(x+n)=x2+mx-32,则m、n的值分别是( )
| A. | 4,8 | B. | 4,-8 | C. | -4,8 | D. | -4,-8 |
7.晓影设计了一个关于实数运算的程序:输入一个数后,输出的数总是比该数的平方小1,晓影按照此程序输入$\sqrt{2012}$后,输出的结果应为( )
| A. | 2010 | B. | 2011 | C. | 2012 | D. | 2013 |
11.下列四个数是负分数的是( )
| A. | -(-0.6$\stackrel{•}{6}$) | B. | π | C. | -$\frac{3}{5}$ | D. | 0.341 |
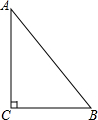 有一块直角三角形的绿地,量得BC、AC两直角边长分别为6m,8m.现在要将绿地扩充成等腰三角形,且要求扩充的绿地部分是以AC为直角边的直角三角形ACD,求扩充后绿地所构成等腰三角形ABD的周长.
有一块直角三角形的绿地,量得BC、AC两直角边长分别为6m,8m.现在要将绿地扩充成等腰三角形,且要求扩充的绿地部分是以AC为直角边的直角三角形ACD,求扩充后绿地所构成等腰三角形ABD的周长.