题目内容
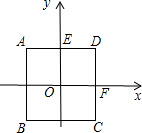如图所示，以正方形ABCD平行于边的对称轴为坐标轴建立直角坐标系，若正方形的边长为4．（1）求过B、E、F三点的二次函数的解析式；
（2）求此抛物线的顶点坐标．（先转化为点的坐标，再求函数解析式）
分析：（1）根据B、E、F三点的坐标，设函数解析式为y=ax2+bx+c，即可求解；
（2）把函数解析式化为顶点式后即可得出答案．
（2）把函数解析式化为顶点式后即可得出答案．
解答：解：（1）由题意知：点B（-2，-2），点E（0，2），点F（2，0），
分别代入y=ax2+bx+c，
解得：a=-
，b=
，c=2，
故函数解析式为：y=-
x2+
x+2；
（2）∵y=-
x2+
x+2=-
(x-
)2+
，
∴顶点坐标为（
，
）．
分别代入y=ax2+bx+c，
解得：a=-
| 3 |
| 4 |
| 1 |
| 2 |
故函数解析式为：y=-
| 3 |
| 4 |
| 1 |
| 2 |
（2）∵y=-
| 3 |
| 4 |
| 1 |
| 2 |
| 3 |
| 4 |
| 1 |
| 3 |
| 25 |
| 12 |
∴顶点坐标为（
| 1 |
| 3 |
| 25 |
| 12 |
点评：本题考查了待定系数法求函数解析式，属于基础题，关键是正确设出二次函数解析式的一般形式．
练习册系列答案
相关题目
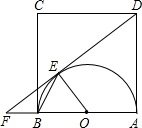B的延长线于点F，BF=4．
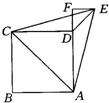16、如图所示，以正方形ABCD的对角线AC为边作等边三角形ACE，过点E作EF⊥AD，交AD的延长线于F，则∠DEF=
已知正方形ABCD的边长为2，点P是BC上的一点，将△DCP沿DP折叠至△DPQ，若DQ，DP恰好与如图所示的以正方形ABCD的中心O为圆心的⊙O相切，则折痕DP的长为（ ）
如图所示，以正方形ABCD中AD边为一边向外作等边△ADE，则∠AEB=（ ）