题目内容
【题目】如图，
是
的斜边
上异于
、
的一定点，过点作直线
截
交
于点
，使截得的
与相似．已知
，
，
，则
________．
【答案】
或
【解析】
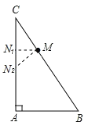
首先利用勾股定理求出BC的长，过点M作直线与另一边相交，因为所得的三角形与原三角形有一个公共角，所以只要再作一个直角就可以使得△CMN与△ABC相似，分别讨论∠CMN=90°和∠CNM=90°两种情况，求出CN的长即可.
如图所示：
∵AB=6，AC=8，∠A=90°，
∴BC=
=10，
过点M作MN1∥AB，则△CMN1∽△CBA，
∴CN1：CA=CM：BC，
即CN1：8：=4：10，
解得：CN1=3.2；
以M为顶点作∠CMN2=∠A=90°，则△CMN2∽△CBA，
所以CN2：BC=CM：AC，
即CN2：10：=4：8，
解得：CN2=5；
综上可知当CN=3.2或8时△CMN与△ABC相似，
故答案为：3.2或5
练习册系列答案
相关题目
