题目内容
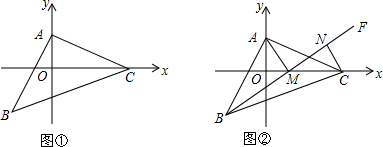
5. 如图,抛物线y=-x2+ax+8(a≠0)于x轴从左到右交于点A,B于y轴交于点C于直线y=kx+b交于点c和点D(m,5),tan∠DCO=1
如图,抛物线y=-x2+ax+8(a≠0)于x轴从左到右交于点A,B于y轴交于点C于直线y=kx+b交于点c和点D(m,5),tan∠DCO=1(1)求抛物线与直线CD的解析式;
(2)在抛物线的对称轴上有点E,使EA+EC的值最小,求最小值和点E的坐标;
(3)点F为在直线CD上方的抛物线上任意一点,作FG⊥CD于点G,作FH∥y轴,与直线CD交于点H,求△FGH的周长的最大值和对应的点F的坐标.
分析 (1)作DM⊥x轴于点M,根据tan∠DCO=1,则∠DCM=45°,△CDM是等腰直角三角形,求得D的坐标,然后利用待定系数法求得抛物线和直线CD的解析式;
(2)首先求得A和B的坐标,以及抛物线的对称轴,直线BC与对称轴的交点就是点E,首先求得BC的解析式,则E的坐标即可求得;
(3)△FGH是等腰直角三角形,当FG最大时,△FGH的周长的最大,设与CD平行,且与抛物线只有一个公共点的直线,利用根的判别式即可求得直线的解析式,进而求得唯一的公共点,即F的坐标,求得△FGH的周长.
解答 解:(1)作DM⊥x轴于点M.
在y=-x2+ax+8中令x=0,则y=8,则C的坐标是(0,8),即OC=8.
∵D的纵坐标是5,
∴M的坐标是(0,5),即OM=5.
∴CM=OC-OM=8-5=3.
∵tan∠DCO=1,
∴∠DCM=45°,则△CDM是等腰三角形.
∴DM=CM=3,
∴D的坐标是(3,5).
把(3,5)代入y=-x2+ax+8得:-9+3a+8=5,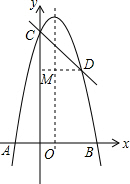
解得:a=2.
则二次函数的解析式是y=-x2+2x+8;
设CD的解析式是y=kx+b,
则$\left\{\begin{array}{l}{3k+b=5}\\{b=8}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-1}\\{b=8}\end{array}\right.$,
则直线CD的解析式是y=-x+8;
(2)抛物线的对称轴是x=1.
在y=-x2+2x+8中,令y=0,则-x2+2x+8=0,解得:x=4或-2.
则A的坐标是(-2,0),B的坐标是(4,0),BC=$\sqrt{{8}^{2}+{4}^{2}}$=4$\sqrt{5}$,EA+EC的值最值是4$\sqrt{5}$.
设BC的解析式是y=dx+e,
则$\left\{\begin{array}{l}{4d+e=0}\\{e=8}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{d=-2}\\{e=8}\end{array}\right.$,
则BC的解析式是y=-2x+8.
令x=1,y=-2+8=6,
则E的坐标是(1,6);
(3)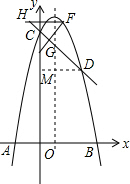 设与CD平行,且与抛物线只有一个公共点的直线解析式是y=-x+d,
设与CD平行,且与抛物线只有一个公共点的直线解析式是y=-x+d,
则-x2+2x+8=-x+d,
即x2-3x+(d-8)=0,
△=9-4(d-8)=0,解得:d=$\frac{41}{4}$.
当d=$\frac{41}{4}$时,x=$\frac{3}{2}$,y=-$\frac{3}{2}$+$\frac{41}{4}$=$\frac{35}{4}$.
则F的坐标是($\frac{3}{2}$,$\frac{35}{4}$).
在y=-x+8中,令y=$\frac{35}{4}$,则-x+8=$\frac{35}{4}$,解得x=-$\frac{3}{4}$,即H的坐标是(-$\frac{3}{4}$,$\frac{35}{4}$).
HF=$\frac{3}{2}$+$\frac{3}{4}$=$\frac{9}{4}$.
则FG=HG=$\frac{\sqrt{2}}{2}$HF=$\frac{\sqrt{2}}{2}$×$\frac{9}{4}$=$\frac{9\sqrt{2}}{8}$,
则△FGH的周长是2×$\frac{9\sqrt{2}}{8}$+$\frac{9}{4}$=$\frac{9(\sqrt{2}+1)}{4}$.
点评 本题考查了待定系数法求函数的解析式,理解直线与抛物线的交点的个数的判断,求得F的坐标是解决本题的关键.

 阅读快车系列答案
阅读快车系列答案 如图,直线l1的函数表达式为y1=-3x+3,且l1与x轴交于点D,直线l2:y2=kx+b经过点A,B,与直线l1交于点C.
如图,直线l1的函数表达式为y1=-3x+3,且l1与x轴交于点D,直线l2:y2=kx+b经过点A,B,与直线l1交于点C. 如图,AC是⊙O的直径,点B是AC延长线上一点,直线BD与⊙O相切于点D.若AD=BD,求证:∠DAB=∠B=30°.
如图,AC是⊙O的直径,点B是AC延长线上一点,直线BD与⊙O相切于点D.若AD=BD,求证:∠DAB=∠B=30°.
 如图,已知∠ACB=90°,CD⊥AB于D,∠1=∠2,EF∥AB,AC=6,BC=8.
如图,已知∠ACB=90°,CD⊥AB于D,∠1=∠2,EF∥AB,AC=6,BC=8. 如图,⊙O半径为4cm,其内接正六边形ABCDEF,点P,Q同时分别从A,D两点出发,以1cm/s速度沿AF,DC向中点F,G运动.连接PB,QE,设运动时间为t(s).
如图,⊙O半径为4cm,其内接正六边形ABCDEF,点P,Q同时分别从A,D两点出发,以1cm/s速度沿AF,DC向中点F,G运动.连接PB,QE,设运动时间为t(s).