题目内容
已知正整数a,b,c满足不等式a2+b2+c2+43≤ab+9b+8c,则a+b+c的值为________.
13
分析:根据正整数a,b,c满足不等式a2+b2+c2+43≤ab+9b+8c,把不等式进行变形为完全平方和的形式,进而可求解.
解答:不等式a2+b2+c2+43≤ab+9b+8c,
∴a2-ab+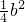 +
+ -9b+27+c2-8c+16≤0,
-9b+27+c2-8c+16≤0,
∴ +3
+3 +(c-4)2≤0,
+(c-4)2≤0,
故a=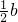 ,
, b=3,c=4,
b=3,c=4,
∴a+b+c=3+6+4=13.
故答案为:13.
点评:本题考查了完全平方公式及非负数的性质,难度适中,关键是根据几个非负数的和小于等于0时,这几个非负数都同时为0.
分析:根据正整数a,b,c满足不等式a2+b2+c2+43≤ab+9b+8c,把不等式进行变形为完全平方和的形式,进而可求解.
解答:不等式a2+b2+c2+43≤ab+9b+8c,
∴a2-ab+
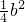 +
+ -9b+27+c2-8c+16≤0,
-9b+27+c2-8c+16≤0,∴
 +3
+3 +(c-4)2≤0,
+(c-4)2≤0,故a=
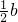 ,
, b=3,c=4,
b=3,c=4,∴a+b+c=3+6+4=13.
故答案为:13.
点评:本题考查了完全平方公式及非负数的性质,难度适中,关键是根据几个非负数的和小于等于0时,这几个非负数都同时为0.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案
相关题目