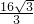题目内容
小明为了测量水面宽度AB，从C点分别测得A，B两点的俯角分别为60°，30°，C点到水面的距离CD=8米，则AB等于（ ）分析：由条件可以求出∠BCD=60°，∠ACD=30°，根据锐角三角函数值解直角三角形就可以求出BD、和AD的值，从而求出AB的值．
解答：
解：∵DC⊥CE，∠BCE=30°，∠ACE=60°，
∴∠BCD=60°，∠ACD=30°
∵tan60°=
=
，tan30°=
=
，CD=8，
∴BD=8
，AD=
，
∴AB=8
-
=
，
∴C答案正确．
故选C．
解：∵DC⊥CE，∠BCE=30°，∠ACE=60°，∴∠BCD=60°，∠ACD=30°
∵tan60°=
| BD |
| CD |
| 3 |
| ||
| 3 |
| AD |
| CD |
∴BD=8
| 3 |
8
| ||
| 3 |
∴AB=8
| 3 |
8
| ||
| 3 |
16
| ||
| 3 |
∴C答案正确．
故选C．
点评：本题是一道解直角三角形的题，考查了仰角、俯角的知识及解直角三角形中正切值的运用．
练习册系列答案
科学实验活动册系列答案
相关题目
小明为了测量水面宽度AB，从C点分别测得A，B两点的俯角分别为60°，30°，C点到水面的距离CD=8米，则AB等于
