题目内容
已知抛物线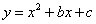 与x轴交于点
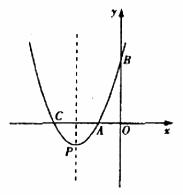
与x轴交于点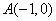 、C,与y轴交于点B(0,3),抛物线的顶点为p。
、C,与y轴交于点B(0,3),抛物线的顶点为p。
(1)求抛物线的解析式;
(2)若抛物线向下平移k个单位后经过点(-5,6)。
①求k的值及平移后抛物线所对应函数的最小值;
②设平移后抛物线与y轴交于点D,顶点为Q,点M是平移后的抛物线上的一个动点。请探究:当点M在何处时,△MBD的而积是△MPQ面积的2倍?求出此时点M的坐标。
解:(1)把(-1,0),(0,3)分别代入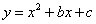

∴抛物线的解析式为
(2)①知平移后抛物线的解析式为
∵抛物线经过点(-5,6),
 ;
;

∴平移后抛物线的解析式为
∴对应函数的最小值是-3
②由①知,BD=PQ=2,抛物线的对称轴为直线 。
。
又
∴△MBD中BD边上的高是△MPQ中PQ边上的高的2倍。
设点M的坐标为 ,
,
a. 当点M在直线 的左侧时,如图,则有
的左侧时,如图,则有 ,
,

 ,
,
 ,
,
 。
。
b. 当点M在直线 与y轴之间时,则有
与y轴之间时,则有
 ,
,

c. 当点M在y轴右侧时,则有
 ,不合题意。
,不合题意。
∴点M的坐标是 或
或

练习册系列答案
相关题目
 中自变量x的取值范围是
中自变量x的取值范围是 B.
B. C.
C. D.
D.
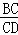 =
= ,则△CEF≌△CDF.
,则△CEF≌△CDF.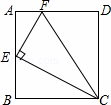
 的解是___________。
的解是___________。
 B.
B. C.
C. D.
D.
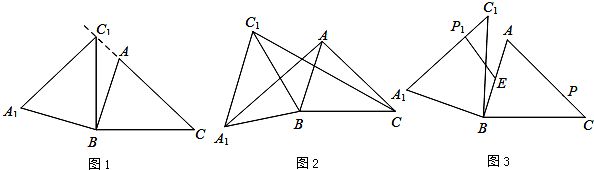 在锐角△ABC中,AB=4,BC=5,∠ACB=45°,将△ABC绕点B按逆时针方向旋转,得到△A1BC1.
在锐角△ABC中,AB=4,BC=5,∠ACB=45°,将△ABC绕点B按逆时针方向旋转,得到△A1BC1. 的对应点是点P1,求线段EP1长度的最大值与最小值.
的对应点是点P1,求线段EP1长度的最大值与最小值.