题目内容
)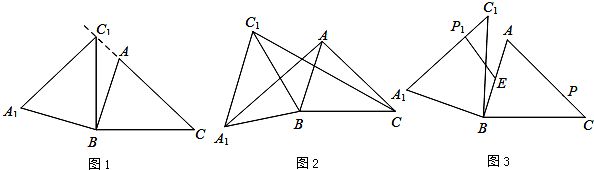 在锐角△ABC中,AB=4,BC=5,∠ACB=45°,将△ABC绕点B按逆时针方向旋转,得到△A1BC1.
在锐角△ABC中,AB=4,BC=5,∠ACB=45°,将△ABC绕点B按逆时针方向旋转,得到△A1BC1.
(1)如图1,当点C1在线段CA的延长线上时,求∠CC1A1的度数;
(2)如图2,连接AA1,CC1.若△ABA1的面积为4,求△CBC1的面积;
(3)如图3,点E为线段AB中点,点P是线段AC上的动点,在△ABC绕点B按逆时针方向旋转过程中,点P 的对应点是点P1,求线段EP1长度的最大值与最小值.
的对应点是点P1,求线段EP1长度的最大值与最小值.
解:(1)由旋转的性质可得∠A1C1B =∠ACB =45°,BC=BC1
∴∠CC1B =∠C1CB =45°
∴∠CC1A1=∠CC1B+∠A1C1B=45°+45°=90°
(2)∵△ABC≌△A1BC1
∴BA=BA1,BC=BC1,∠ABC=∠A1BC1
∴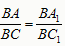 , ∠ABC+∠ABC1=∠A1BC1+∠ABC1
, ∠ABC+∠ABC1=∠A1BC1+∠ABC1
∴∠ABA1=∠CBC1
∴△ABA1∽△CBC1
∴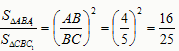
∵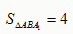
∴
(3)过点B作BD⊥AC,D为垂足
∵△ABC为锐角三角形
∴点D在线段AC上Rt△BCD中,BD=BC×sin45°=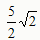
P在AC上运动至垂足点D,△ABC绕点B旋转,
使点P的对应点P1在线段AB上时,EP1最小,最小值为-2② 当P在AC上运动至点C,△ABC绕点B旋转,使点P的对应点P1在线段AB的延长线上时,EP1最大,最大值为2+5=7 。

练习册系列答案
相关题目
在平面直角坐标系中,将抛物线y=3x2先向右平移1个单位,再向上平移2个单位,得到的抛物线的解析式是( )
|
| A. | y=3(x+1)2+2 | B. | y=3(x+1)2﹣2 | C. | y=3(x﹣1)2+2 | D. | y=3(x﹣1)2﹣2 |
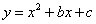 与x轴交于点
与x轴交于点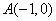 、C,与y轴交于点B(0,3),抛物线的顶点为p。
、C,与y轴交于点B(0,3),抛物线的顶点为p。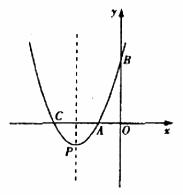
 ,可列方程为 .
,可列方程为 .  正方体组成的几何体,它的俯视图为( )
正方体组成的几何体,它的俯视图为( )
 B.
B. C.
C. D.
D.

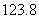 亿元,工程于2009年6月全面开工建设,工期为5年,到2014年通车试运营.
亿元,工程于2009年6月全面开工建设,工期为5年,到2014年通车试运营. 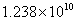 元 (B)
元 (B)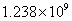 元 (C)
元 (C) 元 (D)
元 (D)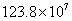 元
元 ,
, 平分
平分 ,若
,若 , 则
, 则 的度数是( ).
的度数是( ).