题目内容
 如图,在长方形ABCD中,AB=5,AC=13,求这个长方形的面积.
如图,在长方形ABCD中,AB=5,AC=13,求这个长方形的面积.考点:勾股定理,矩形的性质
专题:
分析:先根据勾股定理求出BC的长,进而可得出结论.
解答:
解:∵四边形ABCD是长方形,
∴AD=BC,AB⊥BC.
∵AB=5,AC=13,
∴BC=
=12,
∴S矩形ABCD=AB•BC=5×12=60.
∴AD=BC,AB⊥BC.
∵AB=5,AC=13,
∴BC=
| 132-52 |
∴S矩形ABCD=AB•BC=5×12=60.
点评:本题考查的是勾股定理,熟知在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
下列计算正确的是( )
| A、a2+a2=a4 |
| B、a2•a3=a6 |
| C、(ab3)2=ab6 |
| D、a3÷a2=a |

 如图,点A、F、C、D在同一直线上,点B和点E分别在直线AD的两侧,且AB=DE,∠A=∠D,AF=DC.试猜想线段BC和EF的数量及位置关系,并证明你的猜想.
如图,点A、F、C、D在同一直线上,点B和点E分别在直线AD的两侧,且AB=DE,∠A=∠D,AF=DC.试猜想线段BC和EF的数量及位置关系,并证明你的猜想.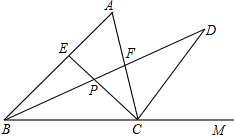 如图所示,在△ABC中∠A=60°,∠ABC的角平分线和∠ACB的外角平分线交于点D,与∠ACB的角平分线交于点P,与边AC交于点F.
如图所示,在△ABC中∠A=60°,∠ABC的角平分线和∠ACB的外角平分线交于点D,与∠ACB的角平分线交于点P,与边AC交于点F.