题目内容
9. 如图,在边长为1个单位长度的小正方形组成的网格中.
如图,在边长为1个单位长度的小正方形组成的网格中.(1)把△ABC进行平移,得到△A′B′C′,使点A与A′对应,请在网格中画出△A′B′C′.
(2)若一个格点多边形的面积记为S,其内部格点数记为N,边界上的格点数记为L.则图中格点△ABC对应的N=3,L=3,S=3.5.
(3)已知格点多边形的面积可表示为S=N+aL+b,且已知当N=1,L=6时,S=3.若某格点多边形对应的N=12,L=8,求S的值.
分析 (1)根据图形平移的性质画出△A′B′C′即可;
(2)根据△ABC内的格点数可得出L的值,同理得出L的值,利用正方形的面积减去三个顶点上三角形的面积即可得出S的值;
(3)求出ab的值,再把N=12,L=8代入进行计算即可.
解答 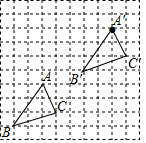 解:(1)如图△A?B?C?即为所求;
解:(1)如图△A?B?C?即为所求;
(2)由图可知N=3,L=3,S=3×3-$\frac{1}{2}$×3×1-$\frac{1}{2}$×2×1-$\frac{1}{2}$×2×3=3.5.
故答案为:3,3,3.5;
(3)∵由题意得$\left\{\begin{array}{l}{3+3a+b=3.5}\\{1+6a+b=3}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=\frac{1}{2}}\\{b=-1}\end{array}\right.$
∴S=N+$\frac{1}{2}$L-1
∴当N=12,L=8时,S=15.
点评 本题考查的是作图-平移变换,熟知图形平移不变性的性质是解答此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
17.下列给出的各组线段中,能构成三角形的是( )
| A. | 5,12,13 | B. | 5,12,7 | C. | 8,18,7 | D. | 3,4,8 |
1.下列说法正确的是( )
| A. | 两数之和必大于任何一个加数 | |
| B. | 同号两数相加,符号不变,并把绝对值相加 | |
| C. | 两负数相加和为负数,并把绝对值相减 | |
| D. | 异号两数相加,取绝对值较大的加数的符号,并把绝对值相加 |
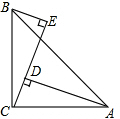 如图,∠ACB=90°,AC=BC,BE⊥CE,AD⊥CE于D,AD=25,BE=8,求DE的长.
如图,∠ACB=90°,AC=BC,BE⊥CE,AD⊥CE于D,AD=25,BE=8,求DE的长.
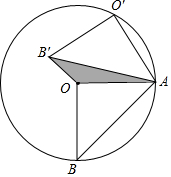 如图,在Rt△AOB中,∠AOB=Rt∠,OA=OB=2,将△AOB绕点A按顺时针旋转至△AO′B′,使点O′落在以O为圆心,OA长为半径的圆上,则△AOB′的面积是$\sqrt{3}$-1.
如图,在Rt△AOB中,∠AOB=Rt∠,OA=OB=2,将△AOB绕点A按顺时针旋转至△AO′B′,使点O′落在以O为圆心,OA长为半径的圆上,则△AOB′的面积是$\sqrt{3}$-1.