题目内容
18.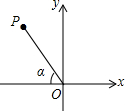 如图,点P在第二象限,OP与x轴负半轴的夹角是α,且OP=5,cosα=$\frac{3}{5}$,则点P坐标是( )
如图,点P在第二象限,OP与x轴负半轴的夹角是α,且OP=5,cosα=$\frac{3}{5}$,则点P坐标是( )| A. | (3,4) | B. | (-3,4) | C. | (-4,3) | D. | (-3,5) |
分析 过点P作PA⊥x轴于点A,过点P作PB⊥y轴于点B,根据OP=5,cosα=$\frac{3}{5}$可求出OA,再根据勾股定理可求出PA,由此即可得出点P的坐标.
解答 解:过点P作PA⊥x轴于点A,过点P作PB⊥y轴于点B,如图所示.
∵OP=5,cosα=$\frac{3}{5}$,
∴OA=OP•cosα=3,PA=$\sqrt{O{P}^{2}-O{A}^{2}}$=4,
∴点P的坐标为(-3,4).
故选B.
点评 本题考查了解直角三角形以及点的坐标,解题的关键是:求出OA,PA的长.本题属于基础题,难度不大,解决该题型题目时,构建直角三角形通过解直角三角形来找出点的坐标是关键.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
9.已知三角形两边的长分别是5和8,则此三角形第三边的长可能是下列的( )
| A. | 3 | B. | 4 | C. | 13 | D. | 14 |
13.某校食堂的中餐与晚餐的资费标准如下:
小杰同学某星期从周一到周五每天的中餐与晚餐均在学校选用A类或B类中的一份套餐菜与一份米饭用餐,这五天共消费36元.请问小杰在这五天内,A,B类套餐菜各选用了多少次?
| 种类 | 单价 |
| 米饭 | 0.5元/份 |
| A类套餐菜 | 3.5元/份 |
| B类套餐菜 | 2.5元/份 |
3.我市某校准备组织学生及学生家长坐高铁到杭州进行社会实践,为了便于管理.所有人员必须乘坐在同一列高铁上.根据报名人数,若都买一等座单程火车票需6560元,若都买二等座单程火车票,则需3120元(学生票二等座打7.5折,一等座不打折).已知学生家长与教师的人数之比为3:1,余姚北站到杭州东站的火车票价格如表所示:
(1)参加社会实践的老师、家长与学生各有多少人?
(2)由于各种原因,二等座火车票单程只能买m张(m小于参加社会实践的人数),其余的须买一等座火车票,在保证每位参与人员都有座位坐的前提下,请你设计最经济的购票方案,并写出购买火车票的总费用(单程)y(元)(用含m的代数式表示).
| 运行区间 | 票价 | ||
| 上车站 | 下车站 | 一等座 | 二等座 |
| 余姚北 | 杭州东 | 82(元) | 48(元) |
(2)由于各种原因,二等座火车票单程只能买m张(m小于参加社会实践的人数),其余的须买一等座火车票,在保证每位参与人员都有座位坐的前提下,请你设计最经济的购票方案,并写出购买火车票的总费用(单程)y(元)(用含m的代数式表示).
 如图,正方形ABCD中,E、F分别是CD、DA的中点.BE与CF相交于点P.
如图,正方形ABCD中,E、F分别是CD、DA的中点.BE与CF相交于点P. 小明给右图建立平面直角坐标系,使医院的坐标为(0,0),火车站的坐标为(2,2),写出体育场、文化宫、超市、宾馆、市场的坐标;并分别指出在第几象限.
小明给右图建立平面直角坐标系,使医院的坐标为(0,0),火车站的坐标为(2,2),写出体育场、文化宫、超市、宾馆、市场的坐标;并分别指出在第几象限. 如图,两个正六边形的面积分别为16,9,两个阴影部分的面积分别为a,b(a<b),则b-a的值为( )
如图,两个正六边形的面积分别为16,9,两个阴影部分的面积分别为a,b(a<b),则b-a的值为( )