题目内容
 如图,BD⊥AC,EF⊥AC,D、F分别为垂足,∠1=∠4.求证:∠ADG=∠C.
如图,BD⊥AC,EF⊥AC,D、F分别为垂足,∠1=∠4.求证:∠ADG=∠C.证明:∵BD⊥AC,EF⊥AC(
∴∠2=∠3=90° (
∴BD∥EF(
∴∠4=
∵∠1=∠4(
∴∠1=
∴DG∥BC(
∴∠ADG=∠C(
考点:平行线的判定与性质
专题:推理填空题
分析:先由垂直的定义得到:∠2=∠3,然后由同位角相等,两直线平行得到:EF∥BD,再由两直线平行,同位角相等得到:∠4=∠5,然后根据等量代换得到:∠1=∠5,再根据内错角相等,两直线平行得到:DG∥BC,最后由两直线平行,同位角相等即可证∠ADG=∠C.
解答:证明:∵BD⊥AC,EF⊥AC(已知)
∴∠2=∠3=90° ( 垂直的定义),
∴BD∥EF(同位角相等,两直线平行)
∴∠4=∠5(两直线平行,同位角相等)
∵∠1=∠4( 已知)
∴∠1=∠5(等量代换)
∴DG∥BC(内错角相等,两直线平行)
∴∠ADG=∠C( 两直线平行,同位角相等)
∴∠2=∠3=90° ( 垂直的定义),
∴BD∥EF(同位角相等,两直线平行)
∴∠4=∠5(两直线平行,同位角相等)
∵∠1=∠4( 已知)
∴∠1=∠5(等量代换)
∴DG∥BC(内错角相等,两直线平行)
∴∠ADG=∠C( 两直线平行,同位角相等)
点评:此题考查了平行线的性质与判定,注意平行线的性质和判定的综合运用.

练习册系列答案
相关题目
 如图所示,已知∠C=∠D=90°,AB=AE,增加下列一个条件(1)AC=AD,(2)BC=ED,(3)∠B=∠E,(4)∠1=∠2,其中能使△ABC≌△AED成立的条件有( )
如图所示,已知∠C=∠D=90°,AB=AE,增加下列一个条件(1)AC=AD,(2)BC=ED,(3)∠B=∠E,(4)∠1=∠2,其中能使△ABC≌△AED成立的条件有( )| A、4个 | B、3个 | C、2个 | D、1个 |
函数y=ax2+ax(其中a>0),在坐标系中的大致图象为( )
A、 |
B、 |
C、 |
D、 |
某班30名学生身高检测结果如下表(单位:米),则该班学生身高的众数是( )
| 身高 | 1.57 | 1.58 | 1.59 | 1.60 | 1.61 | 1.62 | 1.63 | 1.64 |
| 人数 | 2 | 2 | 3 | 3 | 8 | 7 | 3 | 2 |
| A、1.59 | B、1.60 |
| C、1.61 | D、1.62 |
已知下列命题:①若a>0,则|a|=a;②若ma2=na2,则m=n;③线段垂直平分线上的点到这条线段两个端点的距离相等;④等腰三角形的两个底角相等.其中原命题与逆命题均为真命题的个数是( )
| A、1个 | B、2个 | C、3个 | D、4个 |
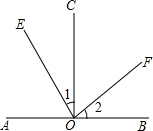 如图,点A,O,B在同一条直线上,∠AOC=∠BOC=90°,∠1=∠2,则图中互余的角共有( )
如图,点A,O,B在同一条直线上,∠AOC=∠BOC=90°,∠1=∠2,则图中互余的角共有( )| A、2对 | B、3对 | C、4对 | D、5对 |