ÌâÄżÄÚÈĘ
ĄŸÌâÄżĄżÄłĐŁŚé֯ѧÉúÊé·š±ÈÈüŁŹ¶ÔČÎÈüŚśÆ·°ŽAĄąBĄąCĄąDËÄžö”ÈŒ¶œűĐĐÁËÆÀ¶šŁźÏÖËæ»úłéÈĄČż·ÖѧÉúÊé·šŚśÆ·”ÄÆÀ¶šœáčûœűĐĐ·ÖÎöŁŹČą»æÖÆÉÈĐÎÍłŒÆÍŒșÍÌőĐÎÍłŒÆÍŒÈçÏÂŁș
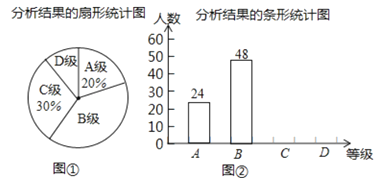
žùŸĘÉÏÊöĐĆÏąÍêłÉÏÂÁĐÎÊÌâŁș
Łš1Ł©ÇóŐâŽÎłéÈĄ”ÄŃù±Ÿ”ÄÈĘÁżŁ»
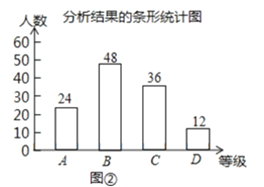
Łš2Ł©ÇëÔÚÍŒąÚÖĐ°ŃÌőĐÎÍłŒÆÍŒČčłäÍêŐûŁ»
Łš3Ł©ÒŃÖȘžĂĐŁŐâŽÎ»î¶ŻčČÊŐ”œČÎÈüŚśÆ·720·ĘŁŹÇëÄăčÀŒÆČÎÈüŚśÆ·Žï”œBŒ¶ÒÔÉÏ(ŒŽAŒ¶șÍBŒ¶)ÓжàÉÙ·ĘŁż
ĄŸŽđ°žĄżŁš1Ł©120Ł»Łš2Ł©ÏêÇéŒûœâÎöŁ»Łš3Ł©432·Ę
ĄŸœâÎöĄż
Łš1Ł©ÀûÓĂAŒ¶”ÄÈËÊęłęÒÔÆäËùŐŒ”İٷֱȜűÒ»ČœŒÆËăÇółöŽđ°žŒŽżÉŁ»
Łš2Ł©ÓĂŐâŽÎ”śČé”ÄŚÜÈËÊęłËÒÔCŒ¶ËùŐŒ”Ä°Ù·Ö±ÈÇółöÏàÓŠ”ÄÈËÊęŁŹÈ»șóœűÒ»ČœÇółöDŒ¶”ÄÈËÊ꣏ÓÉŽËČčÈ«ÌőĐÎÍłŒÆÍŒŒŽżÉŁ»
Łš3Ł©žùŸĘÌâÒâŁŹÊŚÏÈÇółöBŒ¶ÒÔÉÏŐŒ”Ä°Ù·Ö±ÈŁŹÈ»șóœűÒ»ČœłËÒÔ720ŒŽżÉ.
Łš1Ł©ĄßAŒ¶ËùŐŒ”Ä°Ù·Ö±ÈÎȘ![]() ŁŹÆäÈËÊęÎȘ
ŁŹÆäÈËÊęÎȘ![]() ŁŹ
ŁŹ
ĄàŐâŽÎłéÈĄ”ÄŃù±ŸÈĘÁżÎȘŁș![]() ŁŹ
ŁŹ
ŽđŁșŐâŽÎłéÈĄ”ÄŃù±Ÿ”ÄÈĘÁżÎȘ120Ł»
Łš2Ł©žùŸĘCŒ¶ËùŐŒ”Ä°Ù·Ö±ÈżÉ”ĂCŒ¶ÈËÊęÎȘŁș![]() ŁšÈËŁ©ŁŹ
ŁšÈËŁ©ŁŹ
ĄàDŒ¶ÈËÊęÎȘŁș![]() ŁšÈËŁ©ŁŹ
ŁšÈËŁ©ŁŹ
ĄàČčÈ«”ÄÌőĐÎÍłŒÆÍŒÈçÏÂŁș
Łš3Ł©ĄßBŒ¶ÒÔÉÏËùŐŒ”Ä°Ù·Ö±ÈÎȘŁș![]() ŁŹ
ŁŹ
ĄàČÎÈüŚśÆ·Žï”œBŒ¶ÒÔÉϔķĘÊęÎȘŁș![]() Łš·ĘŁ©ŁŹ
Łš·ĘŁ©ŁŹ
ŽđŁșČÎÈüŚśÆ·Žï”œBŒ¶ÒÔÉϔķĘÊęÎȘ432·Ę.

 Êęѧ°ÂÈüÊîŒÙÌìÌìÁ·ÄÏŸ©Žóѧłö°æÉçÏ”ÁĐŽđ°ž
Êęѧ°ÂÈüÊîŒÙÌìÌìÁ·ÄÏŸ©Žóѧłö°æÉçÏ”ÁЎ𰞥ŸÌâÄżĄżŒŃŒŃÏòÌœŸżÒ»ÔȘÈęŽÎ·œłÌx3+2x2©x©2=0”Äœâ”ÄÇéżöŁŹžùŸĘÒÔÍù”ÄŃ§Ï°ŸŃ飏ËûÏ딜ÁË·œłÌÓëșŻÊę”ÄčŰÏ”ŁŹÒ»ŽÎșŻÊęy=kx+bŁškĄÙ0Ł©”ÄÍŒÏóÓëxÖ᜻”ă”ÄșáŚű±êŒŽÎȘÒ»ÔȘÒ»ŽÎ·œłÌkx+bŁškĄÙ0Ł©”ÄœâŁŹ¶țŽÎșŻÊęy=ax2+bx+cŁšaĄÙ0Ł©”ÄÍŒÏóÓëxÖ᜻”ă”ÄșáŚű±êŒŽÎȘÒ»ÔȘ¶țŽÎ·œłÌax2+bx+c=0ŁšaĄÙ0Ł©”ÄœâŁŹÈçŁș¶țŽÎșŻÊęy=x2©2x©3”ÄÍŒÏóÓëxÖá”Äœ»”ăÎȘŁš©1ŁŹ0Ł©șÍŁš3ŁŹ0Ł©ŁŹœ»”ă”ÄșáŚű±ê©1șÍ3ŒŽÎȘx2©2x©3=0”ÄœâŁź
žùŸĘÒÔÉÏ·œłÌÓëșŻÊę”ÄčŰÏ”ŁŹÈçčûÎÒĂÇÖ±”œșŻÊęy=x3+2x2©x©2”ÄÍŒÏóÓëxÖ᜻”ă”ÄșáŚű±êŁŹŒŽżÉÖȘ·œłÌx3+2x2©x©2=0”ÄœâŁź
ŒŃŒŃÎȘÁËœâșŻÊęy=x3+2x2©x©2”ÄÍŒÏóŁŹÍščęĂè”ă·š»łöșŻÊę”ÄÍŒÏóŁź
x | Ą | ©3 | © | ©2 | © | ©1 | © | 0 |
| 1 |
| 2 | Ą |
y | Ą | ©8 | © | 0 |
| m | © | ©2 | © | 0 |
| 12 | Ą |
Łš1Ł©Ö±œÓĐŽłöm”ÄÖ”ŁŹČą»łöșŻÊęÍŒÏóŁ»
Łš2Ł©žùŸĘ±ížńșÍÍŒÏóżÉÖȘŁŹ·œłÌ”ÄœâÓĐĄĄ ĄĄžöŁŹ·Ö±đÎȘĄĄ ĄĄŁ»
Łš3Ł©œèÖúșŻÊę”ÄÍŒÏóŁŹÖ±œÓĐŽłöČ»”ÈÊœx3+2x2ŁŸx+2”ÄœâŒŻŁź