题目内容
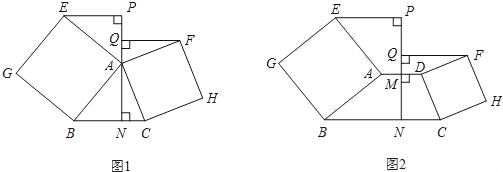
【题目】(1)已知:如图1,△ABC中,分别以AB、AC为一边向△ABC外作正方形ABGE和ACHF,直线AN⊥BC于N,若EP⊥AN于P,FQ⊥AN于Q.判断线段EP、FQ的数量关系,并证明;
(2)如图2,梯形ABCD中,AD∥BC,分别以两腰AB、CD为一边向梯形ABCD外作正方形ABGE和DCHF,线段AD的垂直平分线交线段AD于点M,交BC于点N,若EP⊥MN于P,FQ⊥MN于Q.(1)中结论还成立吗?请说明理由.
【答案】(1)EP、FQ的数量关系是相等,理由见解析;(2)成立,理由见解析
【解析】
(1)由正方形的边角关系可证△FQA≌△ANC,则FQ = AN;同样可证△EPA≌△ANB,则EP= AN,从而得出EP= FQ;
(2)过D作PN的平行线分别交FQ、BC于点K、I,由AAS可证△FKD≌△DIC则QK = DM,
FQ=DM+MN,同理可得,EP=AM+MN,再由MN为AD中垂线,得出AM= MD ,从而证出EP= FQ .
(1)EP、FQ的数量关系是相等.
证明:∠QFA=90°﹣∠FAQ=∠CAN,
在△FQA与△ANC中,
 ,
,
∴△FQA≌△ANC(AAS),
∴FQ=AN;
同理△EPA≌△ANB,
∴EP=AN,
∴EP=FQ;

(2)答:(1)中的结论依然成立.理由如下:
过D作PN的平行线分别交FQ、BC于点K、I.
∵∠KFD=90°﹣∠FDK=∠CDI,
在△FKD与△DIC中,

∴△FKD≌△DIC(AAS),
∴FK=DI,
∴FQ=FK+KQ=DI+DM=DM+MN;
同理可得,EP=AM+MN,
又∵MN为AD中垂线,
∴AM=MD,
∴EP=AM+MN=DM+MN=FQ.

 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案【题目】为声援扬州“运河申遗”,某校举办了一次运河知识竞赛,满分10分,学生得分为整数,成绩达到6分以上(包括6分)为合格,达到9分以上(包含9分)为优秀.这次竞赛中甲乙两组学生成绩分布的条形统计图如图所示.
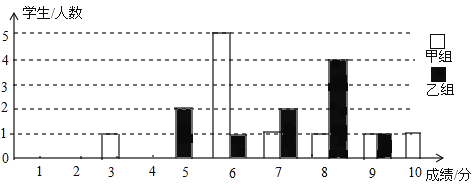
(1)补充完成下面的成绩统计分析表:
组别 | 平均分 | 中位数 | 方差 | 合格率 | 优秀率 |
甲组 | 6.7 | 3.41 | 90% | 20% | |
乙组 | 7.5 | 1.69 | 80% | 10% |
(2)小明同学说:“这次竞赛我得了7分,在我们小组中排名属中游略偏上!”观察上表可知,小明是 组的学生;(填“甲”或“乙”)
(3)甲组同学说他们组的合格率、优秀率均高于乙组,所以他们组的成绩好于乙组.但乙组同学不同意甲组同学的说法,认为他们组的成绩要好于甲组.请你给出两条支持乙组同学观点的理由.