题目内容
9.如果点A(0,1),B(3,1),点C在y轴上,且△ABC的面积是3,则C点坐标(0,-1)或(0,3).分析 根据三角形的面积公式,可得答案.
解答 解:S△ABC=$\frac{1}{2}$AB•|yA-yC|=$\frac{1}{2}$×3|yA-yC|=3,
得|yA-yC|=2,
1-yC=2或1-yC=-2,
解得yC=-1,或yC=3,
C点的坐标是(0,-1)或(0,3).
故答案为:(0,-1)或(0,3).
点评 本题考查了坐标与图形的性质,利用三角形的面积得出|yA-yC|=2是解题关键.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
1.用一个平面去截一个几何体,得到的截面是八边形,这个几何体可能是( )
| A. | 四棱柱 | B. | 五棱柱 | C. | 六棱锥 | D. | 七棱柱 |
 求图中x的值.
求图中x的值.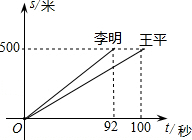 读图填空:如图这是李明、王平两人在一次赛跑中,路程s与时间t的关系,
读图填空:如图这是李明、王平两人在一次赛跑中,路程s与时间t的关系,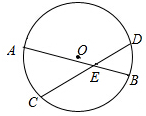 如图,AB,CD是⊙O的两条弦,交于点E,$\widehat{AC}$=80°,$\widehat{BD}$=60°,则∠BED=70°.
如图,AB,CD是⊙O的两条弦,交于点E,$\widehat{AC}$=80°,$\widehat{BD}$=60°,则∠BED=70°.