题目内容
如图,A,B,C分别表示三所不同的学校,B,C在东西向的一条马路边,A学校在B学校北偏西15°方向上,在C学校北偏西60°方向上,A,B两学校之间的距离是1000米,请求出∠BAC的度数以及A,C两学校之间的距离.


【考点】解直角三角形的应用-方向角问题.
【专题】探究型.
【分析】根据题意可以得到∠ABC和∠BCA的度数,从而可以得到∠BAC的度数,作辅助线BD⊥AC,根据题目中的信息可以分别求得AD和CD的长,从而可以得到AC的长.
【解答】解:由已知可得,图形如下,


∵∠ABC=90°+15°=105°,∠ACB=90°﹣60°=30°,
∴∠BAC=180°﹣∠ABC﹣∠ACB=180°﹣105°﹣30°=45°,
作BD⊥AC于点D,如上图所示,
∵∠BDA=90°,∠A=45°,AB=1000,
∴BD=AD=500
 ,
,
又∵∠BDC=90°,∠BCD=30°,BD=500
 ,
,
∴CD=
 ,
,
∴AC=AD+CD=
 ,
,
即∠BAC=45°,A,C两学校之间的距离是(
 )米.
)米.
【点评】本题考查解直角三角形的应用﹣方向角问题,解题的关键是明确题意,找出所求问题需要的条件,作出合适的辅助线,注意辅助线要用虚线.

练习册系列答案
相关题目
 (B)
(B)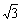 (C)
(C) (D)
(D)





 B.
B.
 C.
C.
 D.
D.





 B.
B.
 C.
C.
 D.
D.


 ,使点A,B在小正方形的顶点上,设AB与网格线相交所成的锐角为α,则不同角度的α有( )
,使点A,B在小正方形的顶点上,设AB与网格线相交所成的锐角为α,则不同角度的α有( )


 x+m(m≥13)交坐标轴于M,N两点,将矩形ABCD沿直线y=﹣
x+m(m≥13)交坐标轴于M,N两点,将矩形ABCD沿直线y=﹣


