题目内容
3. 如图,已知AB∥FD,点E在BC边上,点F在DC的延长线上,且∠AEB=∠F.
如图,已知AB∥FD,点E在BC边上,点F在DC的延长线上,且∠AEB=∠F.(1)求证:△ABE∽△ECF;
(2)若AB=5,CE=6,BE=2,求FC的长.
分析 (1)根据平行四边形的性质得出AB∥CD 故∠1=∠2,再由∠AEB=∠F即可得出结论;
(2)根据相似三角形的对应边成比例即可得出结论.
解答 (1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠1=∠2.
∵∠AEB=∠F,
∴△ABE∽△ECF.
(2)解:∵△ABE∽△ECF,
∴$\frac{AB}{CE}$=$\frac{BE}{CF}$,
∴$\frac{5}{6}$=$\frac{2}{CF}$,
∴CF=$\frac{12}{5}$.
点评 本题考查的是相似三角形的判定与性质,熟知相似三角形的对应边成比例是解答此题的关键.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
13.下列多项式的乘法中可以用平方差公式计算的是( )
| A. | (2x+1)(-2x-1) | B. | (2x+1)(2x+1) | C. | (2x-1)(2x-2) | D. | (-2x+1)(-2x-1) |
14.圆锥的底面半径为4cm,高为3cm,则它的表面积为( )
| A. | 12π cm2 | B. | 20π cm2 | C. | 26π cm2 | D. | 36π cm2 |
18.下图形中,是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
12.已知点(x,y)与点(-2,-3)关于x轴对称,那么x+y=( )
| A. | -5 | B. | 6 | C. | 1 | D. | 5 |
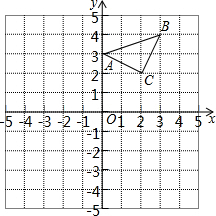 已知,△ABC在直角坐标系内,三个顶点的坐标分别为A(0,3),B(3,4),C(2,2)(正方形网格中每个小正方形的边长均为一个单位长度).
已知,△ABC在直角坐标系内,三个顶点的坐标分别为A(0,3),B(3,4),C(2,2)(正方形网格中每个小正方形的边长均为一个单位长度).