题目内容
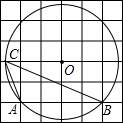如图，⊙O的圆心O在正方形网格中的格点上，A、B两点在⊙O上，并且也在格点上，C为⊙O上一点，∠ACB=45
45
°．分析：连接OA、OB，由图可知OD⊥AB，AD=OD=BD，故△AOD、△BOD均是等腰直角三角形，所以∠AOD=∠BOD=45°，∠AOB=90°，再由圆周角定理即可得出结论．
解答：
解：连接OA、OB，
∵由图可知OD⊥AB，AD=OD=BD，
∴△AOD、△BOD均是等腰直角三角形，
∴∠AOD=∠BOD=45°，
∴∠AOB=∠AOD+∠BOD=45°+45°=90°，
∴∠ACB=
∠AOB=
×90°=45°
故答案为：45．
解：连接OA、OB，∵由图可知OD⊥AB，AD=OD=BD，
∴△AOD、△BOD均是等腰直角三角形，
∴∠AOD=∠BOD=45°，
∴∠AOB=∠AOD+∠BOD=45°+45°=90°，
∴∠ACB=
| 1 |
| 2 |
| 1 |
| 2 |
故答案为：45．
点评：本题考查的是圆周角定理及等腰直角三角形的性质，根据题意作出辅助线，构造出等腰直角三角形是解答此题的关键．
练习册系列答案
相关题目
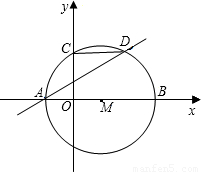
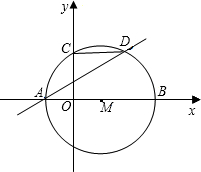轴于点C，弦CD∥x轴交⊙M于点D，已知A、B两点的横坐标分别是方程x2=4（x+3）的两个根，
已知，如图，⊙O2的圆心O2在⊙O1上，且⊙O1与⊙O2的半径均为1，那么阴影部分的面积是
如图，⊙N的圆心N在以AF为直径的⊙M上，⊙M的弦AE所在的直线与⊙N相切于D点，⊙M与⊙N其中的一个交点为C，AC交⊙N于B点，连结NE、AN，设⊙N、⊙M的半径分别为2和3．