题目内容
 如图,⊙N的圆心N在以AF为直径的⊙M上,⊙M的弦AE所在的直线与⊙N相切于D点,⊙M与⊙N其中的一个交点为C,AC交⊙N于B点,连结NE、AN,设⊙N、⊙M的半径分别为2和3.
如图,⊙N的圆心N在以AF为直径的⊙M上,⊙M的弦AE所在的直线与⊙N相切于D点,⊙M与⊙N其中的一个交点为C,AC交⊙N于B点,连结NE、AN,设⊙N、⊙M的半径分别为2和3.(1)求证:AN•NE=12;
(2)若AD=
| 21 |
分析:(1)首先得出A、F、N、E四点在⊙M上,进而得出△DEN∽△NFA,进而得出答案;
(2)利用勾股定理得出AN,FN的长,进而得出cosC=cosF=
,CG=NC•cosC进而得出BC的长.
(2)利用勾股定理得出AN,FN的长,进而得出cosC=cosF=
| ||
| 6 |
解答:(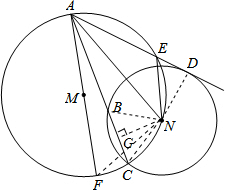 1)证明:连结FN、ND,
1)证明:连结FN、ND,
∵AF为⊙M的直径.AD切⊙N于D点,
∴∠NDE=∠ANF=90°
∵A、F、N、E四点在⊙M上,
∴∠DEN=∠NFA.
∴△DEN∽△NFA,
∴
=
,
∴AN•NE=ND•AF=2×2×3=12;
(2)解:连结NB、NC,过点N作NG⊥BC,垂足为G,
在Rt△AND中,AD=
,DN=2,则AN=5,
在Rt△AFN中,AF=2×3=6,AN=5,则FN=
∴cosC=cosF=
,
在Rt△NGC中,NC=2,
∴CG=NC•cosC=
×2=
∵NB=NC,
∴BC=2CG=2×
=
.
 1)证明:连结FN、ND,
1)证明:连结FN、ND,∵AF为⊙M的直径.AD切⊙N于D点,
∴∠NDE=∠ANF=90°
∵A、F、N、E四点在⊙M上,
∴∠DEN=∠NFA.
∴△DEN∽△NFA,
∴
| ND |
| NE |
| AN |
| AF |
∴AN•NE=ND•AF=2×2×3=12;
(2)解:连结NB、NC,过点N作NG⊥BC,垂足为G,
在Rt△AND中,AD=
| 21 |
在Rt△AFN中,AF=2×3=6,AN=5,则FN=
| 11 |
∴cosC=cosF=
| ||
| 6 |
在Rt△NGC中,NC=2,
∴CG=NC•cosC=
| ||
| 6 |
| ||
| 3 |
∵NB=NC,
∴BC=2CG=2×
| ||
| 3 |
2
| ||
| 3 |
点评:此题主要考查了圆的综合应用以及相似三角形的判定与性质和锐角三角函数关系等知识,利用已知得出CG的长是解题关键.

练习册系列答案
相关题目
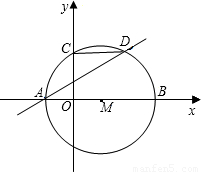
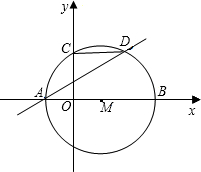 轴于点C,弦CD∥x轴交⊙M于点D,已知A、B两点的横坐标分别是方程x2=4(x+3)的两个根,
轴于点C,弦CD∥x轴交⊙M于点D,已知A、B两点的横坐标分别是方程x2=4(x+3)的两个根, 已知,如图,⊙O2的圆心O2在⊙O1上,且⊙O1与⊙O2的半径均为1,那么阴影部分的面积是
已知,如图,⊙O2的圆心O2在⊙O1上,且⊙O1与⊙O2的半径均为1,那么阴影部分的面积是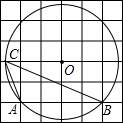 如图,⊙O的圆心O在正方形网格中的格点上,A、B两点在⊙O上,并且也在格点上,C为⊙O上一点,∠ACB=
如图,⊙O的圆心O在正方形网格中的格点上,A、B两点在⊙O上,并且也在格点上,C为⊙O上一点,∠ACB=